In this blog post we work through some examples of computations with crossed product C*-algebras, particularly we look at characterizing *-homomorphisms from a transformation group C*-algebra to a commutative C*-algebra. Some familiarity with C*-crossed products will be assume. Trying to determine all homomorphisms between two given C*-algebra, their algebraic structure, their homotopy classes and so forth, can be quite challenging in general. Most of the standard references on crossed products show how to construct a *-homomorphism of crossed products from an equivariant *-homomorphism of the underlying C*-algebra, but rarely show examples of morphisms that don’t arise in this way.
The example we will look at in this blog post is rather simple though so everything can be computed explicitly. I will be focusing on maps
![Rendered by QuickLaTeX.com \[C(X)\rtimes \Gamma \to C(Y)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-2b18df1f79825f52458d37c59e2cbef1_l3.png)
for two compact Hausdorff spaces  and discrete groups
and discrete groups  . In particular, this covers all characters of
. In particular, this covers all characters of  , and when
, and when  is abelian, also maps of the form
is abelian, also maps of the form
![Rendered by QuickLaTeX.com \[C(X)\rtimes \Gamma \to \C\rtimes \Gamma = C(\hat{\Gamma})\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-6ad70c2a97c6b9a0f6160ce0681686f0_l3.png)
between the C*-algebra

and

where

is a discrete abelian group and

its Pontryagin dual. The reason one may want to study these maps is that for each fixed point of the

action in

we get a *-homomorphism

-equivariant map

, hence they show up quite naturally for actions with fixed points.
For many pathological examples of transformation group C*-algebras see .
1. Notation
Throughout this post  will denote a compact Hausdorff space with a continuous action of
will denote a compact Hausdorff space with a continuous action of  . The crossed product C*-algebra of the dynamical system
. The crossed product C*-algebra of the dynamical system  will be referred to as the transformation group C*-algebra. We will denote by
will be referred to as the transformation group C*-algebra. We will denote by  the fixed points of
the fixed points of  in
in  , meaning the points
, meaning the points  . For now we make no assumptions on this set, but in most cases it will be assumed to be discrete.
. For now we make no assumptions on this set, but in most cases it will be assumed to be discrete.
An element  in the dense subalgebra
in the dense subalgebra  will be denoted by
will be denoted by  where
where  .
.
We denote by  or
or  the action of the group
the action of the group  on a topological space, is continuous function algebra or arbitrary C*-algebras.
on a topological space, is continuous function algebra or arbitrary C*-algebras.
For a *-homomorphism  between two
between two  -dynamical systems, commuting with the
-dynamical systems, commuting with the  -action, we denote by
-action, we denote by  the induced *-homomorphism on the transformation group C*-algebra, defined for a finitely supported function
the induced *-homomorphism on the transformation group C*-algebra, defined for a finitely supported function  by
by
![Rendered by QuickLaTeX.com \[(\phi\otimes id)(\sum f_z u_z ) = \sum \phi(f_z) u_z.\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-29eaa4430d6dd37156e179abddf619d4_l3.png)
If we endow  with the trivial action of of
with the trivial action of of  we get, by functionality of the crossed product, a surjective map
we get, by functionality of the crossed product, a surjective map  for each
for each  -fixed point
-fixed point  , where
, where  is the evaluation at
is the evaluation at  map.
map.
As an example to have in mind, if  we have
we have  and here the homotopy classes of endomorphisms of
and here the homotopy classes of endomorphisms of  is given by
is given by
![Rendered by QuickLaTeX.com \[End(C(\mathbb{T}^n)) = M_n(\Z)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-74d23cc755589b79456adb0f710fd2ee_l3.png)
as any continuous map on  can be approximated by a linear map on the universal cover. This endows the homotopy classes of maps
can be approximated by a linear map on the universal cover. This endows the homotopy classes of maps ![Rendered by QuickLaTeX.com [C(X)\rtimes \Z^n, C(\matbb{T}^n)]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-7e3f56af76965f6f0e7860dcb8ba643e_l3.png) with a right
with a right  action.
action.
Let us first prove the following basic but important result –
Lemma 1 Let

be any discrete group,
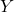
a compact Hausdorff space and

a non-zero *-homomorphism. Then the restriction

is a

-invariant *-homomorphism. In particular if any continuous function

is constant (say

is discrete and
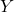
connected) we have
![Rendered by QuickLaTeX.com \[\phi_e = 1\cdot ev_x\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-b4130462fb8b60c9237870df350d2613_l3.png)
for some

.
Now if  is a
is a  -equivariant *-homomorphism between two C*-algebras with respect to two actions of a discrete group
-equivariant *-homomorphism between two C*-algebras with respect to two actions of a discrete group  and
and  is a group homomorphism, we can define a linear map
is a group homomorphism, we can define a linear map
![Rendered by QuickLaTeX.com \[\phi \otimes \rho: C(X)\rtimes_\alpha \Gamma \to C(X)\rtimes_\beta \Gamma\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-d77da948c9dacdfdda34d552210d446f_l3.png)
for any equivariant map

by
![Rendered by QuickLaTeX.com \[\phi\otimes \rho(\sum f_\gamma u_\gamma) = \sum \phi(f)u_{\rho(\gamma)}.\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-61694627145816fcbdaa83ee28cac644_l3.png)
Proof It is a good exercise to check that it preserves products of compactly supported functions, which holds even without the conditions on

. Let us show what goes wrong for the involution, assuming for simplicity that

is unimodular and fill out the details for the general case yourself

However, we also have

Hence we have a  -preserving map if and only if
-preserving map if and only if  , which proves the lemma (modulo details left to the reader).
, which proves the lemma (modulo details left to the reader).
Exercise) Using the above Lemma and our friend the group C*-algebra, show that not all *-homomorphisms of crossed product C*-algebras are induced from equivariant *-homomorphisms of the C*-algebra.
We have so far tacitly ignored the question of boundedness of the above induced maps, since we have been working with the full crossed product. It should be mentioned that for non-effective actions, the question of norm boundedness of the induced map in the above Lemma becomes relevant. For the record, the induced map is bounded in the reduced crossed product if and only if the representation given by composing  with a faithful representation of
with a faithful representation of  is “weakly contained” in the regular representation of
is “weakly contained” in the regular representation of  on
on  .
.
Let us prove the following Lemma –
Lemma 3 Let

be any discrete group. Let

be any

-invariant *-homomorphism and

an arbitrary group homomorphism. Then the map

on

given by
![Rendered by QuickLaTeX.com \[\phi(\sum f_\gamma u_\gamma) := \sum \phi_e(f_\gamma) \phi_\Gamma(u_\gamma)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-132804e8fd3c9ab72806131180029993_l3.png)
determines a *-homomorphism of

. Conversely, all *-homomorphisms

are of this form for a pair of morphisms

and

Proof Let

be a *-homomorphism and

,

its restriction to

and

respectively. Since

and

generate

clearly any *-homomorphism is determined by its values on these subsets and
![Rendered by QuickLaTeX.com \[\phi(\sum f_\gamma u_\gamma) = \sum\phi(f_\gamma) \phi(u_\gamma) = \sum \phi_e(f_\gamma) \phi_\Gamma (u_\gamma).\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-b6fcf45650fbb5c9263dfd9d59219192_l3.png)
Now let  be an arbitrary
be an arbitrary  -invariant *-homomorphism and
-invariant *-homomorphism and  an arbitrary group homomorphism. Then let us show the
an arbitrary group homomorphism. Then let us show the  defined in the lemma is a *-homomorphism. It is linear by construction. Let us check multiplicativity
defined in the lemma is a *-homomorphism. It is linear by construction. Let us check multiplicativity

And *-preserving:
![Rendered by QuickLaTeX.com \begin{align*} \phi((f_\gamma u_\gamma)^*) \\ &= \phi( \alpha_{\gamma^{-1}}(f_\gamma^*) u_\gamma^*) \\ & = \phi_e(\alpha_{\gamma^{-1}}(f_\gamma^*)) \phi_\Gamma(u_\gamma^*) \\ & = \phi_e(f_\gamma^*) \phi_\Gamma(u_\gamma^*) \\ & = [\phi_e(f_\gamma)\phi_\Gamma(u_\gamma)]^* = \phi(f_\gamma u_\gamma)^\star \end{align*}](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-b720140139bedcedda799f0dde52e247_l3.png)
The next Lemma tells us a little more about the homotopy classes of *-homomorphisms:
Lemma 4 Let

be a discrete group with discrete fixed point set and assume
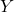
is connected. Then two *-homomorphisms

with corresponding group homomorphisms
![Rendered by QuickLaTeX.com \[\phi_\Gamma, \phi'_\Gamma : \Gamma \to U(C(Y))\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-757277755ebf78b8f6f08c86651edfb7_l3.png)
and algebra *-homomorphisms
![Rendered by QuickLaTeX.com \[\phi_e, \phi'_e :C(X)\to C(Y)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-5812cb1d40ecc694711e0f17c88b8060_l3.png)
are homotopic if and only if

and

is homotopic to

(i.e. there is a family of group homomorphisms

, for
![Rendered by QuickLaTeX.com {t\in [0,1]}](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-911b7e6b8695e5e90aa07f30931ca46f_l3.png)
such that the map

is continuous for all
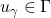
and

,

).
Armed with the above lemmas, we can now prove the following Proposition
Proposition 5 Assume

is finitely generated group with discrete fixed point set and
a connected compact Hausdorff space. Let
![Rendered by QuickLaTeX.com {[C(X)\rtimes \Gamma, C(Y)]}](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-243beebe693d70da6410d9e69f5e5ce2_l3.png)
denote the homotopy classes of *-homomorphisms

. Then there is a 1-1 correspondence
![Rendered by QuickLaTeX.com \[[C(X)\rtimes \Gamma, C(Y)] \leftrightarrow \{(\rho_x)_{x\in Fix_\Gamma(X)} ~|~ \rho_x: \Gamma \to \pi^1(Y)\}\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-697d1c30bf719d91bca840ff3ad07ff7_l3.png)
where
![Rendered by QuickLaTeX.com \[{\pi^1(Y):=U(C(Y))/U(C(Y))_0}\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-eb7809f649cf8cc84ece47dd37302800_l3.png)
is the
cohomotopy group of
.
Proof Let

be the set of generators of

. If

are two group homomorphisms with

and

in the same connected component of

we can continuously deform

to a group homomorphism

for which

. Induction on the set of generators shows

and

are homotopic. The claim now follows easily.
Examples Let us go through some examples. Assume the conditions in the above Corollary are met, then:
- If
 and
and  is abelian, then
is abelian, then
![Rendered by QuickLaTeX.com \[{[C(X)\rtimes \Gamma, \C] \leftrightarrow Fix_\Gamma(X) \times S}\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-106decd233c52998a266b444250463fe_l3.png)
where  is the number of connected components of
is the number of connected components of  . This is because all morphisms are of the form
. This is because all morphisms are of the form  for some character
for some character  . Consequently, if
. Consequently, if  is also torsion-free then
is also torsion-free then
![Rendered by QuickLaTeX.com \[[C(X)\rtimes \Gamma, \C] \leftrightarrow Fix_\Gamma(X).\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-36809ae801d6acdef85573d8fdb4d107_l3.png)
- Similarly, if either
 is perfect or
is perfect or  then
then
![Rendered by QuickLaTeX.com \[[C(X)\rtimes \Gamma, C(Y)] \leftrightarrow Fix_\Gamma(X)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-0e11b7d4b7259a6175e5a9d26ab2f590_l3.png)
in the first case because there are no non-trivial group homomorphisms from  to any abelian group, in the latter because
to any abelian group, in the latter because  , (see this book Section 8.3).
, (see this book Section 8.3).
- Assume
 (or
(or  ) is finitely generated,
) is finitely generated,  is torsion-free with
is torsion-free with  , then
, then
![Rendered by QuickLaTeX.com \[[C(X)\rtimes \Gamma, C(Y)] \leftrightarrow Fix_\Gamma(X)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-0e11b7d4b7259a6175e5a9d26ab2f590_l3.png)
To see this, note the conditions imply there are no non-trivial group homomorphisms  , hence there can be no non-trivial group homomorphism
, hence there can be no non-trivial group homomorphism  where
where  .
.
Here is an more interesting application of the above, for those familiar with symmetric spaces of non-compact type:
Corollary 6 Assume

is a linear algebraic group and

a maximal compact such that

is a symmetric space of non-compact type. Let

be a minimal parabolic subgroup and let

be a maximal flat totally geodesic submanifold of

with

is a lattice in

, hence

where

is the

-rank of

. Let

denote the Weyl group of the (restricted) roots of

. Then
![Rendered by QuickLaTeX.com \[|W| = \#[C(G/P)\rtimes \Gamma_A, \C]\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-e2e71639a39edd5d61deff2b88afc8c6_l3.png)
hence the cardinality of the Weyl group is an isomorphism invariant of

.
Proof It is well known that the Weyl group is in 1-1 correspondence with the fixed points of

in

. Since

is Zariski closed and

is Zariski dense, and the action of

is Zariski continuous it follows that
![Rendered by QuickLaTeX.com \[Fix_A(G/P) = Fix_{\Gamma_A}(G/P).\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-ee2f249aae3b0361075ab1669daba562_l3.png)
The claim now follows from Proposition 5, see also Example 2 above.
More examples of this kind will come shortly, but for this post I think this is a good place to stop.
Bibliography
{6233257:ZPXBQ6GJ}
apa
default
0
4445
%7B%22status%22%3A%22success%22%2C%22updateneeded%22%3Afalse%2C%22instance%22%3Afalse%2C%22meta%22%3A%7B%22request_last%22%3A0%2C%22request_next%22%3A0%2C%22used_cache%22%3Atrue%7D%2C%22data%22%3A%5B%7B%22key%22%3A%22QZ36DEMH%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Szabo%20et%20al.%22%2C%22parsedDate%22%3A%222017-03-23%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESzabo%2C%20G.%2C%20Wu%2C%20J.%2C%20%26amp%3B%20Zacharias%2C%20J.%20%282017%29.%20Rokhlin%20dimension%20for%20actions%20of%20residually%20finite%20groups.%20%3Ci%3EArXiv%3A1408.6096%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1408.6096%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1408.6096%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Rokhlin%20dimension%20for%20actions%20of%20residually%20finite%20groups%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Gabor%22%2C%22lastName%22%3A%22Szabo%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jianchao%22%2C%22lastName%22%3A%22Wu%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joachim%22%2C%22lastName%22%3A%22Zacharias%22%7D%5D%2C%22abstractNote%22%3A%22We%20introduce%20the%20concept%20of%20Rokhlin%20dimension%20for%20actions%20of%20residually%20finite%20groups%20on%20C%2A-algebras%2C%20extending%20previous%20notions%20of%20Rokhlin%20dimension%20for%20actions%20of%20finite%20groups%20and%20the%20integers%2C%20as%20introduced%20by%20Hirshberg%2C%20Winter%20and%20the%20third%20author.%20If%20the%20group%20has%20a%20box%20space%20of%20finite%20asymptotic%20dimension%2C%20then%20actions%20with%20finite%20Rokhlin%20dimension%20preserve%20the%20property%20of%20having%20finite%20nuclear%20dimension%2C%20when%20passing%20to%20the%20crossed%20product%20C%2A-algebra.%20A%20detailed%20study%20of%20the%20asymptotic%20dimension%20of%20box%20spaces%20shows%20that%20finitely%20generated%2C%20virtually%20nilpotent%20groups%20have%20box%20spaces%20with%20finite%20asymptotic%20dimension%2C%20providing%20a%20reasonably%20large%20class%20of%20examples.%20We%20then%20establish%20a%20relation%20between%20Rokhlin%20dimension%20of%20residually%20finite%20groups%20acting%20on%20compact%20metric%20spaces%20and%20amenability%20dimension%20of%20the%20action%20in%20the%20sense%20of%20Guentner%2C%20Willett%20and%20Yu.%20We%20show%20that%20for%20free%20actions%20of%20infinite%2C%20finitely%20generated%2C%20nilpotent%20groups%20on%20finite%20dimensional%20spaces%2C%20both%20these%20dimensional%20values%20are%20finite.%20In%20particular%2C%20the%20associated%20transformation%20group%20C%2A-algebras%20have%20finite%20nuclear%20dimension.%20This%20extends%20an%20analogous%20result%20about%20%24%5C%5Cmathbb%7BZ%7D%5Em%24-actions%20by%20the%20first%20author.%20We%20also%20provide%20some%20results%20concerning%20the%20genericity%20of%20finite%20Rokhlin%20dimension%2C%20and%20permanence%20properties%20with%20respect%20to%20the%20absorption%20of%20a%20strongly%20self-absorbing%20C%2A-algebra.%22%2C%22date%22%3A%222017-03-23%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1408.6096%22%2C%22collections%22%3A%5B%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-27T16%3A16%3A37Z%22%7D%7D%2C%7B%22key%22%3A%22GEN54VRQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Guentner%20et%20al.%22%2C%22parsedDate%22%3A%222015-10-27%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EGuentner%2C%20E.%2C%20Willett%2C%20R.%2C%20%26amp%3B%20Yu%2C%20G.%20%282015%29.%20Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras.%20%3Ci%3EArXiv%3A1510.07769%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Erik%22%2C%22lastName%22%3A%22Guentner%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Rufus%22%2C%22lastName%22%3A%22Willett%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Guoliang%22%2C%22lastName%22%3A%22Yu%22%7D%5D%2C%22abstractNote%22%3A%22We%20introduce%20dynamic%20asymptotic%20dimension%2C%20a%20notion%20of%20dimension%20for%20actions%20of%20discrete%20groups%20on%20locally%20compact%20spaces%2C%20and%20more%20generally%20for%20locally%20compact%20%5C%5C%27etale%20groupoids.%20We%20study%20our%20notion%20for%20minimal%20actions%20of%20the%20integer%20group%2C%20its%20relation%20with%20conditions%20used%20by%20Bartels%2C%20L%5C%5C%5C%22uck%2C%20and%20Reich%20in%20the%20context%20of%20controlled%20topology%2C%20and%20its%20connections%20with%20Gromov%27s%20theory%20of%20asymptotic%20dimension.%20We%20also%20show%20that%20dynamic%20asymptotic%20dimension%20gives%20bounds%20on%20the%20nuclear%20dimension%20of%20Winter%20and%20Zacharias%20for%20C%2A-algebras%20associated%20to%20dynamical%20systems.%20Dynamic%20asymptotic%20dimension%20also%20has%20implications%20for%20K-theory%20and%20manifold%20topology%3A%20these%20will%20be%20drawn%20out%20in%20subsequent%20work.%22%2C%22date%22%3A%222015-10-27%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%22%2C%22collections%22%3A%5B%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-27T16%3A01%3A28Z%22%7D%7D%2C%7B%22key%22%3A%226TLY87YL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Conley%20et%20al.%22%2C%22parsedDate%22%3A%222020-09-14%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EConley%2C%20C.%2C%20Jackson%2C%20S.%2C%20Marks%2C%20A.%2C%20Seward%2C%20B.%2C%20%26amp%3B%20Tucker-Drob%2C%20R.%20%282020%29.%20Borel%20asymptotic%20dimension%20and%20hyperfinite%20equivalence%20relations.%20%3Ci%3EArXiv%3A2009.06721%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2009.06721%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2009.06721%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Borel%20asymptotic%20dimension%20and%20hyperfinite%20equivalence%20relations%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Clinton%22%2C%22lastName%22%3A%22Conley%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Steve%22%2C%22lastName%22%3A%22Jackson%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Andrew%22%2C%22lastName%22%3A%22Marks%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Brandon%22%2C%22lastName%22%3A%22Seward%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robin%22%2C%22lastName%22%3A%22Tucker-Drob%22%7D%5D%2C%22abstractNote%22%3A%22A%20long%20standing%20open%20problem%20in%20the%20theory%20of%20hyperfinite%20equivalence%20relations%20asks%20if%20the%20orbit%20equivalence%20relation%20generated%20by%20a%20Borel%20action%20of%20a%20countable%20amenable%20group%20is%20hyperfinite.%20In%20this%20paper%20we%20prove%20that%20this%20question%20always%20has%20a%20positive%20answer%20when%20the%20acting%20group%20is%20polycyclic%2C%20and%20we%20obtain%20a%20positive%20answer%20for%20all%20free%20actions%20of%20a%20large%20class%20of%20solvable%20groups%20including%20the%20Baumslag--Solitar%20group%20BS%281%2C2%29%20and%20the%20lamplighter%20group.%20This%20marks%20the%20first%20time%20that%20a%20group%20of%20exponential%20volume-growth%20has%20been%20verified%20to%20have%20this%20property.%20In%20obtaining%20this%20result%20we%20introduce%20a%20new%20tool%20for%20studying%20Borel%20equivalence%20relations%20by%20extending%20Gromov%27s%20notion%20of%20asymptotic%20dimension%20to%20the%20Borel%20setting.%20We%20show%20that%20countable%20Borel%20equivalence%20relations%20of%20finite%20Borel%20asymptotic%20dimension%20are%20hyperfinite%2C%20and%20more%20generally%20we%20prove%20under%20a%20mild%20compatibility%20assumption%20that%20increasing%20unions%20of%20such%20equivalence%20relations%20are%20hyperfinite.%20As%20part%20of%20our%20main%20theorem%2C%20we%20prove%20for%20a%20large%20class%20of%20solvable%20groups%20that%20all%20of%20their%20free%20Borel%20actions%20have%20finite%20Borel%20asymptotic%20dimension%20%28and%20finite%20dynamic%20asymptotic%20dimension%20in%20the%20case%20of%20a%20continuous%20action%20on%20a%20zero-dimensional%20space%29.%20We%20also%20provide%20applications%20to%20Borel%20chromatic%20numbers%2C%20Borel%20and%20continuous%20Folner%20tilings%2C%20topological%20dynamics%2C%20and%20%24C%5E%2A%24-algebras.%22%2C%22date%22%3A%222020-09-14%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2009.06721%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%2C%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-27T15%3A53%3A30Z%22%7D%7D%2C%7B%22key%22%3A%22ZLKNIH9X%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Bell%20and%20Dranishnikov%22%2C%22parsedDate%22%3A%222007-04-03%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EBell%2C%20G.%2C%20%26amp%3B%20Dranishnikov%2C%20A.%20%282007%29.%20Asymptotic%20Dimension.%20%3Ci%3EArXiv%3AMath%5C%2F0703766%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0703766%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0703766%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Asymptotic%20Dimension%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22G.%22%2C%22lastName%22%3A%22Bell%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22A.%22%2C%22lastName%22%3A%22Dranishnikov%22%7D%5D%2C%22abstractNote%22%3A%22The%20asymptotic%20dimension%20theory%20was%20founded%20by%20Gromov%20in%20the%20early%2090s.%20In%20this%20paper%20we%20give%20a%20survey%20of%20its%20recent%20history%20where%20we%20emphasize%20two%20of%20its%20features%3A%20an%20analogy%20with%20the%20dimension%20theory%20of%20compact%20metric%20spaces%20and%20applications%20to%20the%20theory%20of%20discrete%20groups.%22%2C%22date%22%3A%222007-04-03%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0703766%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%2C%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-21T18%3A17%3A55Z%22%7D%7D%2C%7B%22key%22%3A%227IDKA7NA%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3Edoi%3A10.1016%5C%2Fj.topol.2008.02.011%20%7C%20Elsevier%20Enhanced%20Reader%3C%5C%2Fi%3E.%20%28n.d.%29.%20https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.topol.2008.02.011%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22webpage%22%2C%22title%22%3A%22doi%3A10.1016%5C%2Fj.topol.2008.02.011%20%7C%20Elsevier%20Enhanced%20Reader%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Freader.elsevier.com%5C%2Freader%5C%2Fsd%5C%2Fpii%5C%2FS0166864108000904%3Ftoken%3D62423AC2F70087FF795AFDCB380A02B6AB4B90A905A2FC9EA3799193623E7D94EF1B01787B838446E60AA45CAEAFA7FD%26originRegion%3Deu-west-1%26originCreation%3D20210921180604%22%2C%22language%22%3A%22en%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-21T18%3A06%3A15Z%22%7D%7D%2C%7B%22key%22%3A%223AS765V2%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Guentner%20et%20al.%22%2C%22parsedDate%22%3A%222015-10-27%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EGuentner%2C%20E.%2C%20Willett%2C%20R.%2C%20%26amp%3B%20Yu%2C%20G.%20%282015%29.%20Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras.%20%3Ci%3EArXiv%3A1510.07769%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Erik%22%2C%22lastName%22%3A%22Guentner%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Rufus%22%2C%22lastName%22%3A%22Willett%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Guoliang%22%2C%22lastName%22%3A%22Yu%22%7D%5D%2C%22abstractNote%22%3A%22We%20introduce%20dynamic%20asymptotic%20dimension%2C%20a%20notion%20of%20dimension%20for%20actions%20of%20discrete%20groups%20on%20locally%20compact%20spaces%2C%20and%20more%20generally%20for%20locally%20compact%20%5C%5C%27etale%20groupoids.%20We%20study%20our%20notion%20for%20minimal%20actions%20of%20the%20integer%20group%2C%20its%20relation%20with%20conditions%20used%20by%20Bartels%2C%20L%5C%5C%5C%22uck%2C%20and%20Reich%20in%20the%20context%20of%20controlled%20topology%2C%20and%20its%20connections%20with%20Gromov%27s%20theory%20of%20asymptotic%20dimension.%20We%20also%20show%20that%20dynamic%20asymptotic%20dimension%20gives%20bounds%20on%20the%20nuclear%20dimension%20of%20Winter%20and%20Zacharias%20for%20C%2A-algebras%20associated%20to%20dynamical%20systems.%20Dynamic%20asymptotic%20dimension%20also%20has%20implications%20for%20K-theory%20and%20manifold%20topology%3A%20these%20will%20be%20drawn%20out%20in%20subsequent%20work.%22%2C%22date%22%3A%222015-10-27%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%5D%2C%22dateModified%22%3A%222021-09-21T18%3A02%3A51Z%22%7D%7D%2C%7B%22key%22%3A%22T7BM3CUF%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Serre%22%2C%22parsedDate%22%3A%221980%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESerre%2C%20J.-P.%20%281980%29.%20Trees%20and%20Amalgams.%20In%20J.-P.%20Serre%2C%20%3Ci%3ETrees%3C%5C%2Fi%3E%20%28pp.%201%26%23x2013%3B68%29.%20Springer%20Berlin%20Heidelberg.%20https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2F978-3-642-61856-7_1%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22bookSection%22%2C%22title%22%3A%22Trees%20and%20Amalgams%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22bookAuthor%22%2C%22firstName%22%3A%22Jean-Pierre%22%2C%22lastName%22%3A%22Serre%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Pierre%22%2C%22lastName%22%3A%22Serre%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22bookTitle%22%3A%22Trees%22%2C%22date%22%3A%221980%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-3-642-61858-1%20978-3-642-61856-7%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2F978-3-642-61856-7_1%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%5D%2C%22dateModified%22%3A%222021-09-21T18%3A02%3A17Z%22%7D%7D%2C%7B%22key%22%3A%225N7BHDP9%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Hill%22%2C%22parsedDate%22%3A%222021-01-16%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EHill%2C%20T.%20P.%20%282021%29.%20An%20Evolutionary%20Theory%20for%20the%20Variability%20Hypothesis.%20%3Ci%3EArXiv%3A1703.04184%20%5Bq-Bio%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1703.04184%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1703.04184%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22An%20Evolutionary%20Theory%20for%20the%20Variability%20Hypothesis%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Theodore%20P.%22%2C%22lastName%22%3A%22Hill%22%7D%5D%2C%22abstractNote%22%3A%22An%20elementary%20biostatistical%20theory%20based%20on%20a%20selectivity-variability%20principle%20is%20proposed%20to%20address%20a%20question%20raised%20by%20Charles%20Darwin%2C%20namely%2C%20how%20one%20sex%20of%20a%20sexually%20dimorphic%20species%20might%20tend%20to%20evolve%20with%20greater%20variability%20than%20the%20other%20sex.%20Briefly%2C%20the%20theory%20says%20that%20if%20one%20sex%20is%20relatively%20selective%20then%20from%20one%20generation%20to%20the%20next%2C%20more%20variable%20subpopulations%20of%20the%20opposite%20sex%20will%20generally%20tend%20to%20prevail%20over%20those%20with%20lesser%20variability.%20Moreover%2C%20the%20perhaps%20less%20intuitive%20converse%20also%20holds%3A%20if%20a%20sex%20is%20relatively%20non-selective%2C%20then%20less%20variable%20subpopulations%20of%20the%20opposite%20sex%20will%20prevail%20over%20those%20with%20greater%20variability.%20This%20theory%20requires%20certain%20regularity%20conditions%20on%20the%20distributions%2C%20but%20makes%20no%20assumptions%20about%20differences%20in%20means%20between%20the%20sexes%2C%20nor%20does%20it%20presume%20that%20one%20sex%20is%20selective%20and%20the%20other%20non-selective.%20Two%20mathematical%20models%20of%20the%20selectivity-variability%20principle%20are%20presented%3A%20a%20discrete-time%20one-step%20probabilistic%20model%20of%20short-term%20behavior%20with%20an%20example%20using%20normally%20distributed%20perceived%20fitness%20values%3B%20and%20a%20continuous-time%20deterministic%20model%20for%20the%20long-term%20asymptotic%20behavior%20of%20the%20expected%20sizes%20of%20the%20subpopulations%20with%20an%20example%20using%20exponentially%20distributed%20fitness%20levels.%22%2C%22date%22%3A%222021-01-16%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1703.04184%22%2C%22collections%22%3A%5B%2222Z435ZZ%22%5D%2C%22dateModified%22%3A%222021-09-17T15%3A43%3A34Z%22%7D%7D%2C%7B%22key%22%3A%22Z5UHF6YS%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Albuquerque%22%2C%22parsedDate%22%3A%221999-03-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EAlbuquerque%2C%20P.%20%281999%29.%20Patterson-Sullivan%20Theory%20in%20Higher%20Rank%20Symmetric%20Spaces.%20%3Ci%3EGeometric%20%26amp%3B%20Functional%20Analysis%20GAFA%3C%5C%2Fi%3E%2C%20%3Ci%3E9%3C%5C%2Fi%3E%281%29%2C%201%26%23x2013%3B28.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs000390050079%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs000390050079%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Patterson-Sullivan%20Theory%20in%20Higher%20Rank%20Symmetric%20Spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22P.%22%2C%22lastName%22%3A%22Albuquerque%22%7D%5D%2C%22abstractNote%22%3A%22Let%20X%20%3D%20G%5C%2FK%20be%20a%20Riemannian%20symmetric%20space%20of%20noncompact%20type%20and%20%24%20%5C%5CGamma%20%24a%20discrete%20%5Cu201cgeneric%5Cu201d%20subgroup%20of%20G%20with%20critical%20exponent%20%24%20%5C%5Cdelta%28%5C%5CGamma%29%20%24.%20Denote%20by%20%24%20X_%7Breg%7D%20%28%5C%5Cinfty%29%20%24the%20set%20of%20regular%20elements%20of%20the%20geometric%20boundary%20%24%20X%28%5C%5Cinfty%29%20%24of%20X.%20We%20show%20that%20the%20support%20of%20all%20%24%20%5C%5CGamma%20%24-invariant%20conformal%20densities%20of%20dimension%20%24%20%5C%5Cdelta%28%5C%5CGamma%29%20%24on%20%24%20X_%7Breg%7D%20%28%5C%5Cinfty%29%20%24%28e.g.%20Patterson-Sullivan%20densities%29%20lie%20in%20a%20same%20and%20single%20regular%20G-orbit%20on%20%24%20X%28%5C%5Cinfty%29%20%24.%20This%20provides%20information%20on%20the%20large-scale%20growth%20of%20%24%20%5C%5CGamma%20%24-orbits%20in%20X.%20If%20in%20addition%20we%20assume%20%24%20%5C%5CGamma%20%24to%20be%20of%20divergence%20type%2C%20then%20there%20is%20a%20unique%20density%20of%20the%20previous%20type.%20Furthermore%2C%20we%20explicitly%20determine%20%24%20%5C%5Cdelta%28%5C%5CGamma%29%20%24and%20this%20G-orbit%20for%20lattices%2C%20and%20show%20that%20they%20are%20of%20divergence%20type.%22%2C%22date%22%3A%221999-03-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs000390050079%22%2C%22ISSN%22%3A%221420-8970%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs000390050079%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-09-06T14%3A17%3A30Z%22%7D%7D%2C%7B%22key%22%3A%22DDWYEVQ6%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kadison%20and%20Ringrose%22%2C%22parsedDate%22%3A%221972%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281972%29.%20Cohomology%20of%20operator%20algebras.%20III%26%23x202F%3B%3A%20reduction%20to%20normal%20cohomology.%20%3Ci%3EBulletin%20de%20la%20Soci%26%23xE9%3Bt%26%23xE9%3B%20Math%26%23xE9%3Bmatique%20de%20France%3C%5C%2Fi%3E%2C%20%3Ci%3E100%3C%5C%2Fi%3E%2C%2073%26%23x2013%3B96.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras.%20III%20%3A%20reduction%20to%20normal%20cohomology%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221972%22%2C%22language%22%3A%22fr%22%2C%22DOI%22%3A%2210.24033%5C%2Fbsmf.1731%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fwww.numdam.org%5C%2Fitem%5C%2F%3Fid%3DBSMF_1972__100__73_0%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-05T14%3A23%3A08Z%22%7D%7D%2C%7B%22key%22%3A%22AFZF3PHG%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kadison%20and%20Ringrose%22%2C%22parsedDate%22%3A%221971-12%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281971%29.%20Cohomology%20of%20operator%20algebras%20II.%20Extended%20cobounding%20and%20the%20hyperfinite%20case.%20%3Ci%3EArkiv%20F%26%23xF6%3Br%20Matematik%3C%5C%2Fi%3E%2C%20%3Ci%3E9%3C%5C%2Fi%3E%281%26%23x2013%3B2%29%2C%2055%26%23x2013%3B63.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02383637%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02383637%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras%20II.%20Extended%20cobounding%20and%20the%20hyperfinite%20case%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22Arkiv%20f%5Cu00f6r%20Matematik%22%2C%22date%22%3A%221971%5C%2F12%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2FBF02383637%22%2C%22ISSN%22%3A%220004-2080%2C%201871-2487%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fprojecteuclid.org%5C%2Fjournals%5C%2Farkiv-for-matematik%5C%2Fvolume-9%5C%2Fissue-1-2%5C%2FCohomology-of-operator-algebras-II-Extended-cobounding-and-the-hyperfinite%5C%2F10.1007%5C%2FBF02383637.full%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-05T14%3A22%3A24Z%22%7D%7D%2C%7B%22key%22%3A%222SVX5YLX%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kadison%20and%20Ringrose%22%2C%22parsedDate%22%3A%221971-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281971%29.%20Cohomology%20of%20operator%20algebras%3A%20I.%20Type%20I%20von%20Neumann%20algebras.%20%3Ci%3EActa%20Mathematica%3C%5C%2Fi%3E%2C%20%3Ci%3E126%3C%5C%2Fi%3E%28none%29%2C%20227%26%23x2013%3B243.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02392032%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02392032%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras%3A%20I.%20Type%20I%20von%20Neumann%20algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22Acta%20Mathematica%22%2C%22date%22%3A%221971%5C%2F01%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2FBF02392032%22%2C%22ISSN%22%3A%220001-5962%2C%201871-2509%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fprojecteuclid.org%5C%2Fjournals%5C%2Facta-mathematica%5C%2Fvolume-126%5C%2Fissue-none%5C%2FCohomology-of-operator-algebras--I-Type-I-von-Neumann%5C%2F10.1007%5C%2FBF02392032.full%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-05T14%3A20%3A58Z%22%7D%7D%2C%7B%22key%22%3A%22ZCEX2Z5M%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pop%20and%20Smith%22%2C%22parsedDate%22%3A%222010-04-15%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EPop%2C%20F.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%282010%29.%20Vanishing%20of%20second%20cohomology%20for%20tensor%20products%20of%20type%20II1%20von%20Neumann%20algebras.%20%3Ci%3EJournal%20of%20Functional%20Analysis%3C%5C%2Fi%3E%2C%20%3Ci%3E258%3C%5C%2Fi%3E%288%29%2C%202695%26%23x2013%3B2707.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.jfa.2010.01.013%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.jfa.2010.01.013%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Vanishing%20of%20second%20cohomology%20for%20tensor%20products%20of%20type%20II1%20von%20Neumann%20algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Florin%22%2C%22lastName%22%3A%22Pop%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22We%20show%20that%20the%20second%20cohomology%20group%20H2%28M%5Cu2297%5Cu00afN%2CM%5Cu2297%5Cu00afN%29%20is%20always%20zero%20for%20arbitrary%20type%20II1%20von%20Neumann%20algebras%20M%20and%20N.%22%2C%22date%22%3A%22April%2015%2C%202010%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.jfa.2010.01.013%22%2C%22ISSN%22%3A%220022-1236%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.sciencedirect.com%5C%2Fscience%5C%2Farticle%5C%2Fpii%5C%2FS002212361000025X%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T19%3A07%3A21Z%22%7D%7D%2C%7B%22key%22%3A%224RNRZD9Y%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Christensen%20et%20al.%22%2C%22parsedDate%22%3A%222003-09-21%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EChristensen%2C%20E.%2C%20Pop%2C%20F.%2C%20Sinclair%2C%20A.%2C%20%26amp%3B%20Smith%2C%20R.%20%282003%29.%20Hochschild%20Cohomology%20Of%20Factors%20With%20Property%20Gamma.%20%3Ci%3EAnnals%20of%20Mathematics%3C%5C%2Fi%3E%2C%20%3Ci%3E158%3C%5C%2Fi%3E%2C%20635%26%23x2013%3B659.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20Cohomology%20Of%20Factors%20With%20Property%20Gamma%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Erik%22%2C%22lastName%22%3A%22Christensen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Florin%22%2C%22lastName%22%3A%22Pop%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20main%20result%20of%20this%20paper%20is%20that%20the%20k%20th%20continuous%20Hochschild%20cohomology%20groups%20H%20k%20%28M%2CM%29%20and%20H%20k%20%28M%2CB%28H%29%29%20of%20a%20von%20Neumann%20factor%20M%20%23%20B%28H%29%20of%20type%20II%201%20with%20property%20%23%20are%20zero%20for%20all%20positive%20integers%20k.%20The%20method%20of%20proof%20involves%20the%20construction%20of%20hyperfinite%20subfactors%20with%20special%20properties%20and%20a%20new%20inequality%20of%20Grothendieck%20type%20for%20multilinear%20maps.%20We%20prove%20joint%20continuity%20in%20the%20%23%20%23%202%20-norm%20of%20separately%20ultraweakly%20continuous%20multilinear%20maps%2C%20and%20combine%20these%20results%20to%20reduce%20to%20the%20case%20of%20completely%20bounded%20cohomology%20which%20is%20already%20solved.%20%23%20Partially%20supported%20by%20a%20Scheme%204%20collaborative%20grant%20from%20the%20London%20Mathematical%20Society.%20%2B%20Partially%20supported%20by%20a%20grant%20from%20the%20National%20Science%20Foundation.%201%22%2C%22date%22%3A%22September%2021%2C%202003%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T18%3A18%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22LNLGCBPB%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3EHochschild%20cohomology%20of%20factors%20with%20property%20%24%5C%5CGamma%24%20%7C%20Annals%20of%20Mathematics%3C%5C%2Fi%3E.%20%28n.d.%29.%20Retrieved%20September%204%2C%202021%2C%20from%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fannals.math.princeton.edu%5C%2F2003%5C%2F158-2%5C%2Fp07%27%3Ehttps%3A%5C%2F%5C%2Fannals.math.princeton.edu%5C%2F2003%5C%2F158-2%5C%2Fp07%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22blogPost%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20factors%20with%20property%20%24%5C%5CGamma%24%20%7C%20Annals%20of%20Mathematics%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22blogTitle%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fannals.math.princeton.edu%5C%2F2003%5C%2F158-2%5C%2Fp07%22%2C%22language%22%3A%22en-US%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A17%3A22Z%22%7D%7D%2C%7B%22key%22%3A%224R2I4SCQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Cameron%22%2C%22parsedDate%22%3A%222009-06-01%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ECameron%2C%20J.%20%282009%29.%20Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras.%20%3Ci%3EProceedings%20of%20the%20Edinburgh%20Mathematical%20Society%3C%5C%2Fi%3E%2C%20%3Ci%3E52%3C%5C%2Fi%3E%2C%20287%26%23x2013%3B295.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jan%22%2C%22lastName%22%3A%22Cameron%22%7D%5D%2C%22abstractNote%22%3A%22In%20this%20paper%20we%20prove%20that%2C%20for%20a%20type-II1%20factor%20N%20with%20a%20Cartan%20maximal%20abelian%20subalgebra%2C%20the%20Hochschild%20cohomology%20groups%20Hn%28N%2CN%29%3D0%20for%20all%20n%5Cu22651.%20This%20generalizes%20the%20result%20of%20Sinclair%20and%20Smith%2C%20who%20proved%20this%20for%20all%20N%20having%20a%20separable%20predual.%22%2C%22date%22%3A%22June%201%2C%202009%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1017%5C%2FS0013091507000053%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T18%3A12%3A58Z%22%7D%7D%2C%7B%22key%22%3A%22AI5Z6XM6%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Cameron%22%2C%22parsedDate%22%3A%222009%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ECameron%2C%20J.%20%282009%29.%20Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras.%20%3Ci%3EProceedings%20of%20the%20Edinburgh%20Mathematical%20Society%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22J.%22%2C%22lastName%22%3A%22Cameron%22%7D%5D%2C%22abstractNote%22%3A%22Abstract%20In%20this%20paper%20we%20prove%20that%2C%20for%20a%20type-II1%20factor%20N%20with%20a%20Cartan%20maximal%20abelian%20subalgebra%2C%20the%20Hochschild%20cohomology%20groups%20Hn%28N%2CN%29%3D0%20for%20all%20n%5Cu22651.%20This%20generalizes%20the%20result%20of%20Sinclair%20and%20Smith%2C%20who%20proved%20this%20for%20all%20N%20having%20a%20separable%20predual.%22%2C%22date%22%3A%222009%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1017%5C%2FS0013091507000053%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A12%3A46Z%22%7D%7D%2C%7B%22key%22%3A%223JBVWD3W%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Johnson%20et%20al.%22%2C%22parsedDate%22%3A%221972%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EJohnson%2C%20B.%20E.%2C%20Kadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281972%29.%20Cohomology%20of%20operator%20algebras.%20III%26%23x202F%3B%3A%20reduction%20to%20normal%20cohomology.%20%3Ci%3EBulletin%20de%20La%20Soci%26amp%3B%23233%3BT%26amp%3B%23233%3B%20Math%26amp%3B%23233%3BMatique%20de%20France%3C%5C%2Fi%3E%2C%20%3Ci%3E79%3C%5C%2Fi%3E%2C%2073%26%23x2013%3B96.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras.%20III%20%3A%20reduction%20to%20normal%20cohomology%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22B.E.%22%2C%22lastName%22%3A%22Johnson%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221972%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.24033%5C%2Fbsmf.1731%22%2C%22ISSN%22%3A%220037-9484%2C%202102-622X%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fwww.numdam.org%5C%2Fitem%3Fid%3DBSMF_1972__100__73_0%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A05%3A55Z%22%7D%7D%2C%7B%22key%22%3A%22DHK3YBPG%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sinclair%20and%20Smith%22%2C%22parsedDate%22%3A%221998%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESinclair%2C%20A.%20M.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%281998%29.%20Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras.%20%3Ci%3EAmerican%20Journal%20of%20Mathematics%3C%5C%2Fi%3E%2C%20%3Ci%3E120%3C%5C%2Fi%3E%285%29%2C%201043%26%23x2013%3B1057.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%27%3Ehttps%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%20M.%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20main%20result%20of%20this%20paper%20is%20that%20%24H%5E%7Bn%7D%28%7B%5C%5Ccal%20M%7D%2C%7B%5C%5Ccal%20M%7D%29%3D0%24%2C%20n%20%5Cu2265%201%2C%20for%20von%20Neumann%20algebras%20%24%7B%5C%5Ccal%20M%7D%24%20with%20Cartan%20subalgebras%20and%20separable%20preduals.%22%2C%22date%22%3A%221998%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%220002-9327%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T18%3A05%3A16Z%22%7D%7D%2C%7B%22key%22%3A%223H57X7HU%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sinclair%20and%20Smith%22%2C%22parsedDate%22%3A%221998%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESinclair%2C%20A.%20M.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%281998%29.%20Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras.%20%3Ci%3EAmerican%20Journal%20of%20Mathematics%3C%5C%2Fi%3E%2C%20%3Ci%3E120%3C%5C%2Fi%3E%285%29%2C%201043%26%23x2013%3B1057.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%27%3Ehttps%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%20M.%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20main%20result%20of%20this%20paper%20is%20that%20%24H%5E%7Bn%7D%28%7B%5C%5Ccal%20M%7D%2C%7B%5C%5Ccal%20M%7D%29%3D0%24%2C%20n%20%5Cu2265%201%2C%20for%20von%20Neumann%20algebras%20%24%7B%5C%5Ccal%20M%7D%24%20with%20Cartan%20subalgebras%20and%20separable%20preduals.%22%2C%22date%22%3A%221998%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%220002-9327%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A04%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22HQNQUFLG%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Qian%20and%20Shen%22%2C%22parsedDate%22%3A%222014-11-12%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EQian%2C%20W.%2C%20%26amp%3B%20Shen%2C%20J.%20%282014%29.%20Hochschild%20cohomology%20of%20type%20II%24_1%24%20von%20Neumann%20algebras%20with%20Property%20%24%5C%5CGamma%24.%20%3Ci%3EArXiv%3A1407.0664%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1407.0664%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1407.0664%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20type%20II%24_1%24%20von%20Neumann%20algebras%20with%20Property%20%24%5C%5CGamma%24%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Wenhua%22%2C%22lastName%22%3A%22Qian%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Junhao%22%2C%22lastName%22%3A%22Shen%22%7D%5D%2C%22abstractNote%22%3A%22In%20this%20paper%2C%20Property%20%24%5C%5CGamma%24%20for%20a%20type%20II%24_%7B1%7D%24%20von%20Neumann%20algebra%20is%20introduced%20as%20a%20generalization%20of%20Murray%20and%20von%20Neumann%27s%20Property%20%24%5C%5CGamma%24%20for%20a%20type%20II%24_%7B1%7D%24%20factor.%20The%20main%20result%20of%20this%20paper%20is%20that%20if%20a%20type%20II%24_%7B1%7D%24%20von%20Neumann%20algebra%20%24%5C%5Cmathcal%7BM%7D%24%20with%20separable%20predual%20has%20Property%20%24%5C%5CGamma%24%2C%20then%20the%20continuous%20Hochschild%20cohomology%20group%20%24H%5E%7Bk%7D%28%5C%5Cmathcal%7BM%7D%2C%20%5C%5Cmathcal%7BM%7D%29%24%20vanishes%20for%20every%20%24k%20%5C%5Cgeq%202%24.%20This%20gives%20a%20generalization%20of%20an%20earlier%20result%20due%20to%20E.%20Christensen%2C%20F.%20Pop%2C%20A.M.%20Sinclair%20and%20R.R.%20Smith.%22%2C%22date%22%3A%222014-11-12%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1407.0664%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T17%3A53%3A21Z%22%7D%7D%2C%7B%22key%22%3A%22T2TTP4WL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sinclair%20and%20Smith%22%2C%22parsedDate%22%3A%221995-03-09%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESinclair%2C%20A.%20M.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%281995%29.%20%3Ci%3EHochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%3C%5C%2Fi%3E.%20Cambridge%20University%20Press.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22Hochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%20M.%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20subject%20of%20this%20book%20is%20the%20continuous%20Hochschild%20cohomology%20of%20dual%20normal%20modules%20over%20a%20von%20Neumann%20algebra.%20The%20authors%20develop%20the%20necessary%20technical%20results%2C%20assuming%20a%20familiarity%20with%20basic%20C%2A-algebra%20and%20von%20Neumann%20algebra%20theory%2C%20including%20the%20decomposition%20into%20types%2C%20but%20no%20prior%20knowledge%20of%20cohomology%20theory%20is%20required%20and%20the%20theory%20of%20completely%20bounded%20and%20multilinear%20operators%20is%20given%20fully.%20Those%20cases%20when%20the%20continuous%20Hochschild%20cohomology%20Hn%28M%2CM%29%20of%20the%20von%20Neumann%20algebra%20M%20over%20itself%20is%20zero%20are%20central%20to%20this%20book.%20The%20material%20in%20this%20book%20lies%20in%20the%20area%20common%20to%20Banach%20algebras%2C%20operator%20algebras%20and%20homological%20algebra%2C%20and%20will%20be%20of%20interest%20to%20researchers%20from%20these%20fields.%22%2C%22date%22%3A%221995-03-09%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-0-521-47880-9%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T17%3A51%3A20Z%22%7D%7D%2C%7B%22key%22%3A%228QR33GYL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3EHochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%20%7C%20Abstract%20analysis%3C%5C%2Fi%3E.%20%28n.d.%29.%20Cambridge%20University%20Press.%20Retrieved%20September%204%2C%202021%2C%20from%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%5C%2Fhochschild-cohomology-von-neumann-algebras%2C%20https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%27%3Ehttps%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%5C%2Fhochschild-cohomology-von-neumann-algebras%2C%20https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22webpage%22%2C%22title%22%3A%22Hochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%20%7C%20Abstract%20analysis%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%5C%2Fhochschild-cohomology-von-neumann-algebras%2C%20https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%22%2C%22language%22%3A%22en%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T17%3A50%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22H3AX2L9L%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Eynard%22%2C%22parsedDate%22%3A%222014-12-12%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EEynard%2C%20B.%20%282014%29.%20A%20short%20overview%20of%20the%20%26%23x201C%3BTopological%20recursion.%26%23x201D%3B%20%3Ci%3EArXiv%3A1412.3286%20%5BHep-Th%2C%20Physics%3AMath-Ph%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1412.3286%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1412.3286%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20short%20overview%20of%20the%20%5C%22Topological%20recursion%5C%22%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22B.%22%2C%22lastName%22%3A%22Eynard%22%7D%5D%2C%22abstractNote%22%3A%22This%20review%20is%20an%20extended%20version%20of%20the%20Seoul%20ICM%202014%20proceedings.It%20is%20a%20short%20overview%20of%20the%20%5C%22topological%20recursion%5C%22%2C%20a%20relation%20appearing%20in%20the%20asymptotic%20expansion%20of%20many%20integrable%20systems%20and%20in%20enumerative%20problems.%20We%20recall%20how%20computing%20large%20size%20asymptotics%20in%20random%20matrices%2C%20has%20allowed%20to%20discover%20some%20fascinating%20and%20ubiquitous%20geometric%20invariants.%20Specializations%20of%20this%20method%20recover%20many%20classical%20invariants%2C%20like%20Gromov--Witten%20invariants%2C%20or%20knot%20polynomials%20%28Jones%2C%20HOMFLY%2C...%29.%20In%20this%20short%20review%2C%20we%20give%20some%20examples%2C%20give%20definitions%2C%20and%20review%20some%20properties%20and%20applications%20of%20the%20formalism.%22%2C%22date%22%3A%222014-12-12%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1412.3286%22%2C%22collections%22%3A%5B%22DX5YKRMR%22%5D%2C%22dateModified%22%3A%222021-09-02T14%3A23%3A02Z%22%7D%7D%2C%7B%22key%22%3A%22RD8GIFC3%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pimsner%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EPimsner%2C%20M.%20V.%20%281986%29.%20KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees.%20%3Ci%3EInventiones%20Mathematicae%3C%5C%2Fi%3E%2C%20%3Ci%3E86%3C%5C%2Fi%3E%283%29%2C%20603%26%23x2013%3B634.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Mihai%20V.%22%2C%22lastName%22%3A%22Pimsner%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2210%5C%2F1986%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2FBF01389271%22%2C%22ISSN%22%3A%220020-9910%2C%201432-1297%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2FBF01389271%22%2C%22collections%22%3A%5B%22K674WRBB%22%5D%2C%22dateModified%22%3A%222021-08-27T13%3A20%3A23Z%22%7D%7D%2C%7B%22key%22%3A%22I924RBCP%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pimsner%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EPimsner%2C%20M.%20%281986%29.%20%3Ci%3EKK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22M.%22%2C%22lastName%22%3A%22Pimsner%22%7D%5D%2C%22abstractNote%22%3A%22Semantic%20Scholar%20extracted%20view%20of%20%5C%22KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%5C%22%20by%20M.%20Pimsner%22%2C%22date%22%3A%221986%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2FBF01389271%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22K674WRBB%22%5D%2C%22dateModified%22%3A%222021-08-27T13%3A19%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22A2CAVRNJ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Rieffel%22%2C%22parsedDate%22%3A%221982%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ERieffel%2C%20M.%20%281982%29.%20%3Ci%3EApplications%20of%20strong%20Morita%20equivalence%20for%20transofrmation%20C%2A-algebras%3C%5C%2Fi%3E.%20%3Ci%3E38%3C%5C%2Fi%3E%281%29.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fmath.berkeley.edu%5C%2F~rieffel%5C%2Fpapers%5C%2Fapplications.pdf%27%3Ehttps%3A%5C%2F%5C%2Fmath.berkeley.edu%5C%2F~rieffel%5C%2Fpapers%5C%2Fapplications.pdf%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Applications%20of%20strong%20Morita%20equivalence%20for%20transofrmation%20C%2A-algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Marc%22%2C%22lastName%22%3A%22Rieffel%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221982%22%2C%22language%22%3A%22English%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fmath.berkeley.edu%5C%2F~rieffel%5C%2Fpapers%5C%2Fapplications.pdf%22%2C%22collections%22%3A%5B%22EIKGB5RV%22%2C%222AUGUVBU%22%5D%2C%22dateModified%22%3A%222021-08-27T13%3A10%3A02Z%22%7D%7D%2C%7B%22key%22%3A%222KMKAXHS%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kloeckner%22%2C%22parsedDate%22%3A%222010%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKloeckner%2C%20B.%20%282010%29.%20Symmetric%20spaces%20of%20higher%20rank%20do%20not%20admit%20differentiable%20compactifications.%20%3Ci%3EMathematische%20Annalen%3C%5C%2Fi%3E%2C%20%3Ci%3E347%3C%5C%2Fi%3E%284%29%2C%20951%26%23x2013%3B961.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-009-0464-z%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-009-0464-z%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Symmetric%20spaces%20of%20higher%20rank%20do%20not%20admit%20differentiable%20compactifications%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Benoit%22%2C%22lastName%22%3A%22Kloeckner%22%7D%5D%2C%22abstractNote%22%3A%22Any%20nonpositively%20curved%20symmetric%20space%20admits%20a%20topological%20compactification%2C%20namely%20the%20Hadamard%20compactification.%20For%20rank%20one%20spaces%2C%20this%20topological%20compactification%20can%20be%20endowed%20with%20a%20differentiable%20structure%20such%20that%20the%20action%20of%20the%20isometry%20group%20is%20differentiable.%20Moreover%2C%20the%20restriction%20of%20the%20action%20on%20the%20boundary%20leads%20to%20a%20flat%20model%20for%20some%20geometry%20%28conformal%2C%20CR%20or%20quaternionic%20CR%20depending%20of%20the%20space%29.%20One%20can%20ask%20whether%20such%20a%20differentiable%20compactification%20exists%20for%20higher%20rank%20spaces%2C%20hopefully%20leading%20to%20some%20knew%20geometry%20to%20explore.%20In%20this%20paper%20we%20answer%20negatively.%22%2C%22date%22%3A%228%5C%2F2010%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2Fs00208-009-0464-z%22%2C%22ISSN%22%3A%220025-5831%2C%201432-1807%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F0912.0814%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-25T16%3A16%3A24Z%22%7D%7D%2C%7B%22key%22%3A%22SHPJMPC8%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Paradan%22%2C%22parsedDate%22%3A%222009%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EParadan%2C%20P.-E.%20%282009%29.%20Symmetric%20spaces%20of%20the%20non-compact%20type%3A%20Lie%20groups.%20%3Ci%3ES%26%23xE9%3Bminaires%20et%20Congr%26%23xE8%3Bs%3C%5C%2Fi%3E%2C%20%3Ci%3EG%26%23xE9%3Bom%26%23xE9%3Btries%20%26%23xE0%3B%20courbure%20n%26%23xE9%3Bgative%20ou%20nulle%2C%20groupes%20discrets%20et%20rigidit%26%23xE9%3Bs%3C%5C%2Fi%3E%2818%29%2C%2039%26%23x2013%3B76.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00773255%27%3Ehttps%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00773255%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Symmetric%20spaces%20of%20the%20non-compact%20type%3A%20Lie%20groups%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Paul-Emile%22%2C%22lastName%22%3A%22Paradan%22%7D%5D%2C%22abstractNote%22%3A%22In%20these%20notes%2C%20we%20give%20first%20a%20brief%20account%20to%20the%20theory%20of%20Lie%20groups.%20Then%20we%20consider%20the%20case%20of%20a%20smooth%20manifold%20with%20a%20Lie%20group%20of%20symmetries.%20When%20the%20Lie%20group%20acts%20transitively%20%28e.g.%20the%20manifold%20is%20homogeneous%29%2C%20we%20study%20the%20%28affine%29%20invariant%20connections%20on%20it.%20We%20end%20up%20with%20the%20particuler%20case%20of%20homogeneous%20spaces%20which%20are%20the%20symmetric%20spaces%20of%20the%20non-compact%20type.%22%2C%22date%22%3A%222009%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00773255%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-25T16%3A10%3A49Z%22%7D%7D%2C%7B%22key%22%3A%2256Z6HFVV%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Connes%20and%20Skandalis%22%2C%22parsedDate%22%3A%221984-12-31%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EConnes%2C%20A.%2C%20%26amp%3B%20Skandalis%2C%20G.%20%281984%29.%20The%20Longitudinal%20Index%20Theorem%20for%20Foliations.%20%3Ci%3EPublications%20of%20the%20Research%20Institute%20for%20Mathematical%20Sciences%3C%5C%2Fi%3E%2C%20%3Ci%3E20%3C%5C%2Fi%3E%286%29%2C%201139%26%23x2013%3B1183.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2977%5C%2Fprims%5C%2F1195180375%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2977%5C%2Fprims%5C%2F1195180375%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20Longitudinal%20Index%20Theorem%20for%20Foliations%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alain%22%2C%22lastName%22%3A%22Connes%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Georges%22%2C%22lastName%22%3A%22Skandalis%22%7D%5D%2C%22abstractNote%22%3A%22%7C%20published%20in%20Publications%20of%20the%20Research%20Institute%20for%20Mathematical%20Sciences%22%2C%22date%22%3A%221984%5C%2F12%5C%2F31%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.2977%5C%2Fprims%5C%2F1195180375%22%2C%22ISSN%22%3A%220034-5318%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fems.press%5C%2Fjournals%5C%2Fprims%5C%2Farticles%5C%2F3203%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%2C%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-08-25T13%3A55%3A09Z%22%7D%7D%2C%7B%22key%22%3A%22FN5G4KSP%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Schroeder%22%2C%22parsedDate%22%3A%222010-12-06%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESchroeder%2C%20M.%20%282010%29.%20Patterson-Sullivan%20distributions%20for%20symmetric%20spaces%20of%20the%20noncompact%20type.%20%3Ci%3EArXiv%3A1012.1113%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1012.1113%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1012.1113%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Patterson-Sullivan%20distributions%20for%20symmetric%20spaces%20of%20the%20noncompact%20type%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Michael%22%2C%22lastName%22%3A%22Schroeder%22%7D%5D%2C%22abstractNote%22%3A%22We%20generalize%20parts%20of%20a%20special%20non-Euclidean%20calculus%20of%20pseudodifferential%20operators%2C%20which%20was%20invented%20by%20S.%20Zelditch%20for%20hyperbolic%20surfaces%2C%20to%20symmetric%20spaces%20%24X%3DG%5C%2FK%24%20of%20the%20noncompact%20type%20and%20their%20compact%20quotients%20%24Y%3D%5C%5CGamma%5C%5Cbackslash%20G%5C%2FK%24.%20We%20sometimes%20restrict%20our%20results%20to%20the%20case%20of%20rank%20one%20symmetric%20spcaes.%20The%20non-Euclidean%20setting%20extends%20the%20defintion%20of%20so-called%20Patterson-Sullivan%20distributions%2C%20which%20were%20first%20defined%20by%20N.%20Anantharaman%20and%20S.%20Zelditch%20for%20hyperbolic%20systems%2C%20in%20a%20natural%20way%20to%20arbitrary%20symmetric%20spaces%20of%20the%20noncompact%20type.%20We%20find%20an%20explicit%20intertwining%20operator%20mapping%20Patterson-Sullivan%20distributions%20into%20Wigner%20distributions.%20We%20study%20the%20important%20invariance%20and%20equivariance%20properties%20of%20these%20distributions.%20Finally%2C%20we%20describe%20asymptotic%20properties%20of%20these%20distributions.%22%2C%22date%22%3A%222010-12-06%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1012.1113%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-20T10%3A02%3A02Z%22%7D%7D%2C%7B%22key%22%3A%2222BQI6XJ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Helgason%22%2C%22parsedDate%22%3A%221979-02-09%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EHelgason%2C%20S.%20%281979%29.%20%3Ci%3EDifferential%20Geometry%2C%20Lie%20Groups%2C%20and%20Symmetric%20Spaces%3C%5C%2Fi%3E.%20Academic%20Press.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22Differential%20Geometry%2C%20Lie%20Groups%2C%20and%20Symmetric%20Spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sigurdur%22%2C%22lastName%22%3A%22Helgason%22%7D%5D%2C%22abstractNote%22%3A%22The%20present%20book%20is%20intended%20as%20a%20textbook%20and%20reference%20work%20on%20three%20topics%20in%20the%20title.%20Together%20with%20a%20volume%20in%20progress%20on%20%5C%22Groups%20and%20Geometric%20Analysis%5C%22%20it%20supersedes%20my%20%5C%22Differential%20Geometry%20and%20Symmetric%20Spaces%2C%5C%22%20published%20in%201962.%20Since%20that%20time%20several%20branches%20of%20the%20subject%2C%20particularly%20the%20function%20theory%20on%20symmetric%20spaces%2C%20have%20developed%20substantially.%20I%20felt%20that%20an%20expanded%20treatment%20might%20now%20be%20useful.%22%2C%22date%22%3A%221979-02-09%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-0-08-087396-1%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22WNJPFJYS%22%5D%2C%22dateModified%22%3A%222021-08-20T09%3A53%3A20Z%22%7D%7D%2C%7B%22key%22%3A%22VRQJE2KE%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Emerson%20and%20Meyer%22%2C%22parsedDate%22%3A%222006%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EEmerson%2C%20H.%2C%20%26amp%3B%20Meyer%2C%20R.%20%282006%29.%20Euler%20characteristics%20and%20Gysin%20sequences%20for%20group%20actions%20on%20boundaries.%20%3Ci%3EMathematische%20Annalen%3C%5C%2Fi%3E%2C%20%3Ci%3E334%3C%5C%2Fi%3E%284%29%2C%20853%26%23x2013%3B904.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-005-0747-y%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-005-0747-y%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Euler%20characteristics%20and%20Gysin%20sequences%20for%20group%20actions%20on%20boundaries%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Heath%22%2C%22lastName%22%3A%22Emerson%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ralf%22%2C%22lastName%22%3A%22Meyer%22%7D%5D%2C%22abstractNote%22%3A%22Let%20G%20be%20a%20locally%20compact%20group%2C%20let%20X%20be%20a%20universal%20proper%20G-space%2C%20and%20let%20Z%20be%20a%20G-equivariant%20compactification%20of%20X%20that%20is%20H-equivariantly%20contractible%20for%20each%20compact%20subgroup%20H%20of%20G.%20Let%20W%20be%20the%20resulting%20boundary.%20Assuming%20the%20Baum-Connes%20conjecture%20for%20G%20with%20coefficients%20C%20and%20C%28W%29%2C%20we%20construct%20an%20exact%20sequence%20that%20computes%20the%20map%20on%20K-theory%20induced%20by%20the%20embedding%20of%20the%20reduced%20group%20C%2A-algebra%20of%20G%20into%20the%20crossed%20product%20of%20G%20by%20C%28W%29.%20This%20exact%20sequence%20involves%20the%20equivariant%20Euler%20characteristic%20of%20X%2C%20which%20we%20study%20using%20an%20abstract%20notion%20of%20Poincare%20duality%20in%20bivariant%20K-theory.%20As%20a%20consequence%2C%20if%20G%20is%20torsion-free%20and%20the%20Euler%20characteristic%20of%20the%20orbit%20space%20X%5C%2FG%20is%20non-zero%2C%20then%20the%20unit%20element%20of%20the%20boundary%20crossed%20product%20is%20a%20torsion%20element%20whose%20order%20is%20equal%20to%20the%20absolute%20value%20of%20the%20Euler%20characteristic%20of%20X%5C%2FG.%20Furthermore%2C%20we%20get%20a%20new%20proof%20of%20a%20theorem%20of%20Lueck%20and%20Rosenberg%20concerning%20the%20class%20of%20the%20de%20Rham%20operator%20in%20equivariant%20K-homology.%22%2C%22date%22%3A%224%5C%2F2006%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2Fs00208-005-0747-y%22%2C%22ISSN%22%3A%220025-5831%2C%201432-1807%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0505050%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A44%3A27Z%22%7D%7D%2C%7B%22key%22%3A%22TMAT2AZQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Blackadar%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EBlackadar%2C%20B.%20%281986%29.%20%3Ci%3EK-Theory%20for%20Operator%20Algebras%3C%5C%2Fi%3E.%20Springer-Verlag.%20https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2F978-1-4613-9572-0%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22K-Theory%20for%20Operator%20Algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Bruce%22%2C%22lastName%22%3A%22Blackadar%22%7D%5D%2C%22abstractNote%22%3A%22K%20-Theory%20has%20revolutionized%20the%20study%20of%20operator%20algebras%20in%20the%20last%20few%20years.%20As%20the%20primary%20component%20of%20the%20subject%20of%20%5C%22noncommutative%20topol%5Cu00ad%20ogy%2C%5C%22%20K%20-theory%20has%20opened%20vast%20new%20vistas%20within%20the%20structure%20theory%20of%20C%2A%5Cu00ad%20algebras%2C%20as%20well%20as%20leading%20to%20profound%20and%20unexpected%20applications%20of%20opera%5Cu00ad%20tor%20algebras%20to%20problems%20in%20geometry%20and%20topology.%20As%20a%20result%2C%20many%20topolo%5Cu00ad%20gists%20and%20operator%20algebraists%20have%20feverishly%20begun%20trying%20to%20learn%20each%20others%27%20subjects%2C%20and%20it%20appears%20certain%20that%20these%20two%20branches%20of%20mathematics%20have%20become%20deeply%20and%20permanently%20intertwined.%20Despite%20the%20fact%20that%20the%20whole%20subject%20is%20only%20about%20a%20decade%20old%2C%20operator%20K%20-theory%20has%20now%20reached%20a%20state%20of%20relative%20stability.%20While%20there%20will%20undoubtedly%20be%20many%20more%20revolutionary%20developments%20and%20applications%20in%20the%20future%2C%20it%20appears%20the%20basic%20theory%20has%20more%20or%20less%20reached%20a%20%5C%22final%20form.%5C%22%20But%20because%20of%20the%20newness%20of%20the%20theory%2C%20there%20has%20so%20far%20been%20no%20comprehensive%20treatment%20of%20the%20subject.%20It%20is%20the%20ambitious%20goal%20of%20these%20notes%20to%20fill%20this%20gap.%20We%20will%20develop%20the%20K%20-theory%20of%20Banach%20algebras%2C%20the%20theory%20of%20extensions%20of%20C%2A-algebras%2C%20and%20the%20operator%20K%20-theory%20of%20Kasparov%20from%20scratch%20to%20its%20most%20advanced%20aspects.%20We%20will%20not%20treat%20applications%20in%20detail%3B%20however%2C%20we%20will%20outline%20the%20most%20striking%20of%20the%20applications%20to%20date%20in%20a%20section%20at%20the%20end%2C%20as%20well%20as%20mentioning%20others%20at%20suitable%20points%20in%20the%20text.%22%2C%22date%22%3A%221986%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-1-4613-9574-4%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.springer.com%5C%2Fgp%5C%2Fbook%5C%2F9781461395744%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%2C%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A42%3A29Z%22%7D%7D%2C%7B%22key%22%3A%22NT438QC5%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ji%20and%20Macpherson%22%2C%22parsedDate%22%3A%222002%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EJi%2C%20L.%2C%20%26amp%3B%20Macpherson%2C%20R.%20%282002%29.%20Geometry%20of%20compactifications%20of%20locally%20symmetric%20spaces.%20%3Ci%3EAnnales%20de%20l%26%23x2019%3Binstitut%20Fourier%3C%5C%2Fi%3E%2C%20%3Ci%3E52%3C%5C%2Fi%3E%282%29%2C%20457%26%23x2013%3B559.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5802%5C%2Faif.1893%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5802%5C%2Faif.1893%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Geometry%20of%20compactifications%20of%20locally%20symmetric%20spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lizhen%22%2C%22lastName%22%3A%22Ji%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%22%2C%22lastName%22%3A%22Macpherson%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222002%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.5802%5C%2Faif.1893%22%2C%22ISSN%22%3A%220373-0956%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Faif.centre-mersenne.org%5C%2Fitem%5C%2FAIF_2002__52_2_457_0%5C%2F%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%2C%22ATJ7BNSA%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A38%3A11Z%22%7D%7D%2C%7B%22key%22%3A%2242JKA9XK%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A3%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3ENote%20series%3C%5C%2Fi%3E.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22document%22%2C%22title%22%3A%22Note%20series%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A37%3A28Z%22%7D%7D%2C%7B%22key%22%3A%22KYNUWHLL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22parsedDate%22%3A%222021%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%282021%29.%20%3Ci%3EThe%20Karpelevic%20compactification%3C%5C%2Fi%3E.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22document%22%2C%22title%22%3A%22The%20Karpelevic%20compactification%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222021%22%2C%22language%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A36%3A17Z%22%7D%7D%2C%7B%22key%22%3A%2246VA6ZKL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%28N.d.%29.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A32%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22ZSHTDFU3%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Jin%22%2C%22parsedDate%22%3A%222021-07-28%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EJin%2C%20X.%20%282021%29.%20Homological%20Mirror%20Symmetry%20for%20the%20universal%20centralizers%20I%3A%20The%20adjoint%20group%20case.%20%3Ci%3EArXiv%3A2107.13395%20%5BMath-Ph%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2107.13395%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2107.13395%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Homological%20Mirror%20Symmetry%20for%20the%20universal%20centralizers%20I%3A%20The%20adjoint%20group%20case%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Xin%22%2C%22lastName%22%3A%22Jin%22%7D%5D%2C%22abstractNote%22%3A%22We%20prove%20homological%20mirror%20symmetry%20for%20the%20universal%20centralizer%20%24J_G%24%20%28a.k.a%20Toda%20space%29%2C%20associated%20to%20any%20complex%20semisimple%20Lie%20group%20%24G%24.%20The%20A-side%20is%20a%20partially%20wrapped%20Fukaya%20category%20on%20%24J_G%24%2C%20and%20the%20B-side%20is%20the%20category%20of%20coherent%20sheaves%20on%20the%20categorical%20quotient%20of%20a%20dual%20maximal%20torus%20by%20the%20Weyl%20group%20action%20%28with%20some%20modification%20if%20%24G%24%20has%20a%20nontrivial%20center%29.%20This%20is%20the%20first%20and%20the%20main%20part%20of%20a%20two-part%20series%2C%20dealing%20with%20%24G%24%20of%20adjoint%20type.%20The%20general%20case%20will%20be%20proved%20in%20the%20forthcoming%20second%20part%20%5BJin2%5D.%22%2C%22date%22%3A%222021-07-28%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2107.13395%22%2C%22collections%22%3A%5B%22WNJPFJYS%22%5D%2C%22dateModified%22%3A%222021-07-30T13%3A12%3A13Z%22%7D%7D%2C%7B%22key%22%3A%22JUAPTIL6%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Soule%22%2C%22parsedDate%22%3A%222004-03%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESoule%2C%20C.%20%282004%29.%20%3Ci%3EAn%20introduction%20to%20arithmetic%20groups%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00001348%27%3Ehttps%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00001348%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22manuscript%22%2C%22title%22%3A%22An%20introduction%20to%20arithmetic%20groups%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Christophe%22%2C%22lastName%22%3A%22Soule%22%7D%5D%2C%22abstractNote%22%3A%22Arithmetic%20groups%20are%20groups%20of%20matrices%20with%20integral%20entries.We%20shall%20first%20discuss%20their%20origin%20in%20number%20theory%20%28Gauss%2C%20Minkowski%29and%20their%20role%20in%20the%20%5C%22reduction%20theory%20of%20quadratic%20forms%5C%22.Then%20we%20shall%20describe%20these%20groups%20by%20generators%20and%20relations.The%20next%20topic%20will%20be%3A%20are%20all%20subgroups%20of%20finite%20indexgiven%20by%20congruence%20conditions%3F%20Finally%2C%20we%20shall%20discuss%20rigidityproperties%20of%20arithmetic%20groups.%22%2C%22manuscriptType%22%3A%22%22%2C%22date%22%3A%22March%202004%22%2C%22language%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00001348%22%2C%22collections%22%3A%5B%22GBBXXUW9%22%5D%2C%22dateModified%22%3A%222021-06-29T13%3A05%3A15Z%22%7D%7D%2C%7B%22key%22%3A%222II5QJSK%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Rosenberg%20and%20Schochet%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ERosenberg%2C%20J.%20M.%2C%20%26amp%3B%20Schochet%2C%20C.%20%281986%29.%20%3Ci%3EThe%20K%26%23xFC%3Bnneth%20theorem%20and%20the%20universal%20coefficient%20theorem%20for%20equivariant%20K-theory%20and%20KK-theory%3C%5C%2Fi%3E.%20American%20Mathematical%20Society.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22The%20K%5Cu00fcnneth%20theorem%20and%20the%20universal%20coefficient%20theorem%20for%20equivariant%20K-theory%20and%20KK-theory%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%20M.%22%2C%22lastName%22%3A%22Rosenberg%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Claude%22%2C%22lastName%22%3A%22Schochet%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221986%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-0-8218-2349-1%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-06-29T12%3A45%3A39Z%22%7D%7D%2C%7B%22key%22%3A%22G3RECNDH%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Rieffel%22%2C%22parsedDate%22%3A%222002%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ERieffel%2C%20M.%20A.%20%282002%29.%20Group%20C%26%23x2217%3B-Algebras%20as%20Compact%20Quantum%20Metric%20Spaces.%20%3Ci%3EDocumenta%20Mathematica%3C%5C%2Fi%3E%2C%2048.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Group%20C%5Cu2217-Algebras%20as%20Compact%20Quantum%20Metric%20Spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Marc%20A%22%2C%22lastName%22%3A%22Rieffel%22%7D%5D%2C%22abstractNote%22%3A%22Let%20be%20a%20length%20function%20on%20a%20group%20G%2C%20and%20let%20M%20denote%20the%20operator%20of%20pointwise%20multiplication%20by%20on%202%28G%29.%20Following%20Connes%2C%20M%20can%20be%20used%20as%20a%20%5Cu201cDirac%5Cu201d%20operator%20for%20Cr%5Cu2217%28G%29.%20It%20de%5Cufb01nes%20a%20Lipschitz%20seminorm%20on%20Cr%5Cu2217%28G%29%2C%20which%20de%5Cufb01nes%20a%20metric%20on%20the%20state%20space%20of%20Cr%5Cu2217%28G%29.%20We%20investigate%20whether%20the%20topology%20from%20this%20metric%20coincides%20with%20the%20weak-%5Cu2217%20topology%20%28our%20de%5Cufb01nition%20of%20a%20%5Cu201ccompact%20quantum%20metric%20space%5Cu201d%29.%20We%20give%20an%20a%5Cufb03rmative%20answer%20for%20G%20%3D%20Zd%20when%20is%20a%20word-length%2C%20or%20the%20restriction%20to%20Zd%20of%20a%20norm%20on%20Rd.%20This%20works%20for%20Cr%5Cu2217%28G%29%20twisted%20by%20a%202-cocycle%2C%20and%20thus%20for%20noncommutative%20tori.%20Our%20approach%20involves%20Connes%5Cu2019%20cosphere%20algebra%2C%20and%20an%20interesting%20compacti%5Cufb01cation%20of%20metric%20spaces%20which%20is%20closely%20related%20to%20geodesic%20rays.%22%2C%22date%22%3A%222002%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22FHEYZTAY%22%2C%22ATJ7BNSA%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A33%3A30Z%22%7D%7D%2C%7B%22key%22%3A%22CUCW4QLQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20Compactifications%20of%20symmetric%20spaces%20and%20their%20applications.%20%3Ci%3EX%20.%3C%5C%2Fi%3E%2C%2052.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Compactifications%20of%20symmetric%20spaces%20and%20their%20applications%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%224CDSADIM%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A28%3A54Z%22%7D%7D%2C%7B%22key%22%3A%22BDAWEY5Q%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3EAn%20example%20of%20the%20index%20of%20a%20Rockland%20operator%20on%20a%20contact%20manifold%3C%5C%2Fi%3E.%2068.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22An%20example%20of%20the%20index%20of%20a%20Rockland%20operator%20on%20a%20contact%20manifold%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%224CDSADIM%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A27%3A46Z%22%7D%7D%2C%7B%22key%22%3A%22P9CQSSC9%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3EA%20simple%20proof%20of%20the%20Hard%20Lefschetz%20theorem%3C%5C%2Fi%3E.%2037.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20simple%20proof%20of%20the%20Hard%20Lefschetz%20theorem%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%224CDSADIM%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A25%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22HRD52D7X%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3EPensum%20MATH4450%20Videreg%26%23x2DA%3Baende%20Funksjonal%20analyse%20V%26%23x2DA%3Bar%202017%3C%5C%2Fi%3E.%2022.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Pensum%20MATH4450%20Videreg%5Cu02daaende%20Funksjonal%20analyse%20V%5Cu02daar%202017%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22no%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22KVPR5BHZ%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A01%3A56Z%22%7D%7D%2C%7B%22key%22%3A%22CG5RATGZ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3EVidereg%26%23xE5%3Bende%20Funksjonalanalyse%3C%5C%2Fi%3E.%20%28n.d.%29.%20Retrieved%20June%2022%2C%202021%2C%20from%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.overleaf.com%5C%2Fproject%5C%2F59920ace6080cd3eb133870e%27%3Ehttps%3A%5C%2F%5C%2Fwww.overleaf.com%5C%2Fproject%5C%2F59920ace6080cd3eb133870e%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22webpage%22%2C%22title%22%3A%22Videreg%5Cu00e5ende%20Funksjonalanalyse%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22An%20online%20LaTeX%20editor%20that%27s%20easy%20to%20use.%20No%20installation%2C%20real-time%20collaboration%2C%20version%20control%2C%20hundreds%20of%20LaTeX%20templates%2C%20and%20more.%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.overleaf.com%5C%2Fproject%5C%2F59920ace6080cd3eb133870e%22%2C%22language%22%3A%22en%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-06-22T15%3A00%3A49Z%22%7D%7D%5D%7D
Szabo, G., Wu, J., & Zacharias, J. (2017). Rokhlin dimension for actions of residually finite groups.
ArXiv:1408.6096 [Math].
http://arxiv.org/abs/1408.6096
Guentner, E., Willett, R., & Yu, G. (2015). Dynamic Asymptotic Dimension: relation to dynamics, topology, coarse geometry, and $C^*$-algebras.
ArXiv:1510.07769 [Math].
http://arxiv.org/abs/1510.07769
Conley, C., Jackson, S., Marks, A., Seward, B., & Tucker-Drob, R. (2020). Borel asymptotic dimension and hyperfinite equivalence relations.
ArXiv:2009.06721 [Math].
http://arxiv.org/abs/2009.06721
Bell, G., & Dranishnikov, A. (2007). Asymptotic Dimension.
ArXiv:Math/0703766.
http://arxiv.org/abs/math/0703766
doi:10.1016/j.topol.2008.02.011 | Elsevier Enhanced Reader. (n.d.). https://doi.org/10.1016/j.topol.2008.02.011
Guentner, E., Willett, R., & Yu, G. (2015). Dynamic Asymptotic Dimension: relation to dynamics, topology, coarse geometry, and $C^*$-algebras.
ArXiv:1510.07769 [Math].
http://arxiv.org/abs/1510.07769
Serre, J.-P. (1980). Trees and Amalgams. In J.-P. Serre, Trees (pp. 1–68). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-61856-7_1
Hill, T. P. (2021). An Evolutionary Theory for the Variability Hypothesis.
ArXiv:1703.04184 [q-Bio].
http://arxiv.org/abs/1703.04184
Albuquerque, P. (1999). Patterson-Sullivan Theory in Higher Rank Symmetric Spaces.
Geometric & Functional Analysis GAFA,
9(1), 1–28.
https://doi.org/10.1007/s000390050079
Kadison, R. V., & Ringrose, J. R. (1972). Cohomology of operator algebras. III : reduction to normal cohomology.
Bulletin de la Société Mathématique de France,
100, 73–96.
https://doi.org/10.24033/bsmf.1731
Kadison, R. V., & Ringrose, J. R. (1971). Cohomology of operator algebras II. Extended cobounding and the hyperfinite case.
Arkiv För Matematik,
9(1–2), 55–63.
https://doi.org/10.1007/BF02383637
Kadison, R. V., & Ringrose, J. R. (1971). Cohomology of operator algebras: I. Type I von Neumann algebras.
Acta Mathematica,
126(none), 227–243.
https://doi.org/10.1007/BF02392032
Pop, F., & Smith, R. R. (2010). Vanishing of second cohomology for tensor products of type II1 von Neumann algebras.
Journal of Functional Analysis,
258(8), 2695–2707.
https://doi.org/10.1016/j.jfa.2010.01.013
Christensen, E., Pop, F., Sinclair, A., & Smith, R. (2003). Hochschild Cohomology Of Factors With Property Gamma. Annals of Mathematics, 158, 635–659.
Hochschild cohomology of factors with property $\Gamma$ | Annals of Mathematics. (n.d.). Retrieved September 4, 2021, from
https://annals.math.princeton.edu/2003/158-2/p07
Cameron, J. (2009). Hochschild cohomology of II1 factors with Cartan maximal abelian subalgebras.
Proceedings of the Edinburgh Mathematical Society,
52, 287–295.
https://doi.org/10.1017/S0013091507000053
Cameron, J. (2009). Hochschild cohomology of II1 factors with Cartan maximal abelian subalgebras.
Proceedings of the Edinburgh Mathematical Society.
https://doi.org/10.1017/S0013091507000053
Johnson, B. E., Kadison, R. V., & Ringrose, J. R. (1972). Cohomology of operator algebras. III : reduction to normal cohomology.
Bulletin de La SociéTé MathéMatique de France,
79, 73–96.
https://doi.org/10.24033/bsmf.1731
Sinclair, A. M., & Smith, R. R. (1998). Hochschild Cohomology for Von Neumann Algebras with Cartan Subalgebras.
American Journal of Mathematics,
120(5), 1043–1057.
https://www.jstor.org/stable/25098635
Sinclair, A. M., & Smith, R. R. (1998). Hochschild Cohomology for Von Neumann Algebras with Cartan Subalgebras.
American Journal of Mathematics,
120(5), 1043–1057.
https://www.jstor.org/stable/25098635
Qian, W., & Shen, J. (2014). Hochschild cohomology of type II$_1$ von Neumann algebras with Property $\Gamma$.
ArXiv:1407.0664 [Math].
http://arxiv.org/abs/1407.0664
Sinclair, A. M., & Smith, R. R. (1995). Hochschild Cohomology of Von Neumann Algebras. Cambridge University Press.
Eynard, B. (2014). A short overview of the “Topological recursion.”
ArXiv:1412.3286 [Hep-Th, Physics:Math-Ph].
http://arxiv.org/abs/1412.3286
Pimsner, M. V. (1986). KK-groups of crossed products by groups acting on trees.
Inventiones Mathematicae,
86(3), 603–634.
https://doi.org/10.1007/BF01389271
Pimsner, M. (1986).
KK-groups of crossed products by groups acting on trees.
https://doi.org/10.1007/BF01389271
Rieffel, M. (1982).
Applications of strong Morita equivalence for transofrmation C*-algebras.
38(1).
https://math.berkeley.edu/~rieffel/papers/applications.pdf
Kloeckner, B. (2010). Symmetric spaces of higher rank do not admit differentiable compactifications.
Mathematische Annalen,
347(4), 951–961.
https://doi.org/10.1007/s00208-009-0464-z
Paradan, P.-E. (2009). Symmetric spaces of the non-compact type: Lie groups.
Séminaires et Congrès,
Géométries à courbure négative ou nulle, groupes discrets et rigidités(18), 39–76.
https://hal.archives-ouvertes.fr/hal-00773255
Connes, A., & Skandalis, G. (1984). The Longitudinal Index Theorem for Foliations.
Publications of the Research Institute for Mathematical Sciences,
20(6), 1139–1183.
https://doi.org/10.2977/prims/1195180375
Schroeder, M. (2010). Patterson-Sullivan distributions for symmetric spaces of the noncompact type.
ArXiv:1012.1113 [Math].
http://arxiv.org/abs/1012.1113
Helgason, S. (1979). Differential Geometry, Lie Groups, and Symmetric Spaces. Academic Press.
Emerson, H., & Meyer, R. (2006). Euler characteristics and Gysin sequences for group actions on boundaries.
Mathematische Annalen,
334(4), 853–904.
https://doi.org/10.1007/s00208-005-0747-y
Blackadar, B. (1986). K-Theory for Operator Algebras. Springer-Verlag. https://doi.org/10.1007/978-1-4613-9572-0
Ji, L., & Macpherson, R. (2002). Geometry of compactifications of locally symmetric spaces.
Annales de l’institut Fourier,
52(2), 457–559.
https://doi.org/10.5802/aif.1893
Ulsnaes, T. (n.d.). Note series.
Ulsnaes, T. (2021). The Karpelevic compactification.
Jin, X. (2021). Homological Mirror Symmetry for the universal centralizers I: The adjoint group case.
ArXiv:2107.13395 [Math-Ph].
http://arxiv.org/abs/2107.13395
Soule, C. (2004).
An introduction to arithmetic groups.
https://hal.archives-ouvertes.fr/hal-00001348
Rosenberg, J. M., & Schochet, C. (1986). The Künneth theorem and the universal coefficient theorem for equivariant K-theory and KK-theory. American Mathematical Society.
Rieffel, M. A. (2002). Group C∗-Algebras as Compact Quantum Metric Spaces. Documenta Mathematica, 48.
Ulsnaes, T. (n.d.). Compactifications of symmetric spaces and their applications. X ., 52.
Ulsnaes, T. (n.d.). An example of the index of a Rockland operator on a contact manifold. 68.
Ulsnaes, T. (n.d.). A simple proof of the Hard Lefschetz theorem. 37.
Ulsnaes, T. (n.d.). Pensum MATH4450 Videreg˚aende Funksjonal analyse V˚ar 2017. 22.
Videregående Funksjonalanalyse. (n.d.). Retrieved June 22, 2021, from
https://www.overleaf.com/project/59920ace6080cd3eb133870e
![]()
![]() and discrete groups
and discrete groups ![]() . In particular, this covers all characters of
. In particular, this covers all characters of ![]() , and when
, and when ![]() is abelian, also maps of the form
is abelian, also maps of the form![]()
![]() will denote a compact Hausdorff space with a continuous action of
will denote a compact Hausdorff space with a continuous action of ![]() . The crossed product C*-algebra of the dynamical system
. The crossed product C*-algebra of the dynamical system ![]() will be referred to as the transformation group C*-algebra. We will denote by
will be referred to as the transformation group C*-algebra. We will denote by ![]() the fixed points of
the fixed points of ![]() in
in ![]() , meaning the points
, meaning the points ![]() . For now we make no assumptions on this set, but in most cases it will be assumed to be discrete.
. For now we make no assumptions on this set, but in most cases it will be assumed to be discrete.![]() in the dense subalgebra
in the dense subalgebra ![]() will be denoted by
will be denoted by ![]() where
where ![]() .
.![]() or
or ![]() the action of the group
the action of the group ![]() on a topological space, is continuous function algebra or arbitrary C*-algebras.
on a topological space, is continuous function algebra or arbitrary C*-algebras.![]() between two
between two ![]() -dynamical systems, commuting with the
-dynamical systems, commuting with the ![]() -action, we denote by
-action, we denote by ![]() the induced *-homomorphism on the transformation group C*-algebra, defined for a finitely supported function
the induced *-homomorphism on the transformation group C*-algebra, defined for a finitely supported function ![]() by
by ![]()
![]() with the trivial action of of
with the trivial action of of ![]() we get, by functionality of the crossed product, a surjective map
we get, by functionality of the crossed product, a surjective map ![]() for each
for each ![]() -fixed point
-fixed point ![]() , where
, where ![]() is the evaluation at
is the evaluation at ![]() map.
map.![]() we have
we have ![]() and here the homotopy classes of endomorphisms of
and here the homotopy classes of endomorphisms of ![]() is given by
is given by![]()
![]() can be approximated by a linear map on the universal cover. This endows the homotopy classes of maps
can be approximated by a linear map on the universal cover. This endows the homotopy classes of maps ![]() with a right
with a right ![]() action.
action. ![]()
![]()
![]()
![]() and
and ![]() which forces
which forces ![]() to be
to be ![]() -invariant.
-invariant.![]() for some continuous map
for some continuous map ![]() , equivariance of
, equivariance of ![]() is equivalent to
is equivalent to ![]()
![]() is just the evaluation map if
is just the evaluation map if ![]() is constant.
is constant. ![]() is a
is a ![]() -equivariant *-homomorphism between two C*-algebras with respect to two actions of a discrete group
-equivariant *-homomorphism between two C*-algebras with respect to two actions of a discrete group ![]() and
and ![]() is a group homomorphism, we can define a linear map
is a group homomorphism, we can define a linear map ![]()
![]()
 for all
for all  , where
, where  is the action of
is the action of  on
on  .
. descends to a the identity map
descends to a the identity map ![Rendered by QuickLaTeX.com {id = [\rho]: G/H \to G/H}](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-1ddaffbada51ae7f0a48a0e7a3c6c828_l3.png) , where
, where  is the intersection of all stabilizer subgroups.
is the intersection of all stabilizer subgroups.![]() is effective this only holds if
is effective this only holds if ![]() .
.
![]()
![]() -preserving map if and only if
-preserving map if and only if ![]() , which proves the lemma (modulo details left to the reader).
, which proves the lemma (modulo details left to the reader). ![]() with a faithful representation of
with a faithful representation of ![]() is “weakly contained” in the regular representation of
is “weakly contained” in the regular representation of ![]() on
on ![]() .
.![]()
![]()
![]() be an arbitrary
be an arbitrary ![]() -invariant *-homomorphism and
-invariant *-homomorphism and ![]() an arbitrary group homomorphism. Then let us show the
an arbitrary group homomorphism. Then let us show the ![]() defined in the lemma is a *-homomorphism. It is linear by construction. Let us check multiplicativity
defined in the lemma is a *-homomorphism. It is linear by construction. Let us check multiplicativity 
![Rendered by QuickLaTeX.com \begin{align*} \phi((f_\gamma u_\gamma)^*) \\ &= \phi( \alpha_{\gamma^{-1}}(f_\gamma^*) u_\gamma^*) \\ & = \phi_e(\alpha_{\gamma^{-1}}(f_\gamma^*)) \phi_\Gamma(u_\gamma^*) \\ & = \phi_e(f_\gamma^*) \phi_\Gamma(u_\gamma^*) \\ & = [\phi_e(f_\gamma)\phi_\Gamma(u_\gamma)]^* = \phi(f_\gamma u_\gamma)^\star \end{align*}](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-b720140139bedcedda799f0dde52e247_l3.png)
![]()
![]()
![]() is a group homomorphism for which there is a homotopy
is a group homomorphism for which there is a homotopy ![]() between them. Then define
between them. Then define ![]() for some
for some ![]() -invariant
-invariant ![]() . By the previous Lemma,
. By the previous Lemma, ![]() extends to a *-homomorphism
extends to a *-homomorphism ![]() for each
for each ![]() .
.![]() and fix
and fix ![]() . If
. If ![]() , then it is easy to check that
, then it is easy to check that ![]() , hence
, hence ![]() is continuous if
is continuous if ![]() . Assume now that
. Assume now that ![]() for some sequence
for some sequence ![]() . For an arbitrary
. For an arbitrary ![]() we pick
we pick ![]() large enough so that
large enough so that ![]() . Then since *-homomorphisms are contractive, we have
. Then since *-homomorphisms are contractive, we have ![]()
![]() , hence the convergence is
, hence the convergence is ![]() is uniform in
is uniform in ![]() . We can thus us Moore-Osgood’s theorem to interchange the limits
. We can thus us Moore-Osgood’s theorem to interchange the limits ![]()
![]() is continuous for any
is continuous for any ![]() .
. ![]()
![]()
 and
and  is abelian, then
is abelian, then ![Rendered by QuickLaTeX.com \[{[C(X)\rtimes \Gamma, \C] \leftrightarrow Fix_\Gamma(X) \times S}\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-106decd233c52998a266b444250463fe_l3.png)
 is the number of connected components of
is the number of connected components of  . This is because all morphisms are of the form
. This is because all morphisms are of the form  for some character
for some character  . Consequently, if
. Consequently, if  is also torsion-free then
is also torsion-free then ![Rendered by QuickLaTeX.com \[[C(X)\rtimes \Gamma, \C] \leftrightarrow Fix_\Gamma(X).\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-36809ae801d6acdef85573d8fdb4d107_l3.png)
 is perfect or
is perfect or  then
then ![Rendered by QuickLaTeX.com \[[C(X)\rtimes \Gamma, C(Y)] \leftrightarrow Fix_\Gamma(X)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-0e11b7d4b7259a6175e5a9d26ab2f590_l3.png)
 to any abelian group, in the latter because
to any abelian group, in the latter because  , (see this book Section 8.3).
, (see this book Section 8.3).  (or
(or  ) is finitely generated,
) is finitely generated,  is torsion-free with
is torsion-free with  , then
, then ![Rendered by QuickLaTeX.com \[[C(X)\rtimes \Gamma, C(Y)] \leftrightarrow Fix_\Gamma(X)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-0e11b7d4b7259a6175e5a9d26ab2f590_l3.png)
 , hence there can be no non-trivial group homomorphism
, hence there can be no non-trivial group homomorphism  where
where  .
.![]()
![]()
