In this very short post, we look at the properties of a certain bump function of the collection of all geodesic rays emanating from a fixed point 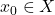 towards irregular points on the geodesic boundary
towards irregular points on the geodesic boundary 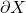 of a non-compact symmetric space
of a non-compact symmetric space
Assume we are given a non-compact symmetric spaces  , and a point
, and a point 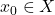 . If
. If  is a geodesic in
is a geodesic in  with
with  , let
, let  be a normal neighborhood of
be a normal neighborhood of  constructed as the parallel translates along
constructed as the parallel translates along  of a fixed ball
of a fixed ball  . We can easily construct a bump function
. We can easily construct a bump function ![Rendered by QuickLaTeX.com s: X\to [0,1]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-886069710c15323a112f37425d5d896a_l3.png) with the following properties
with the following properties
- the function
 only depends on the distance from
only depends on the distance from  ,
,
- the function
 is zero on
is zero on  and
and  on a neighborhood of
on a neighborhood of  .
.
In the case  is the real hyperbolic plane, with the Poincare disc model and
is the real hyperbolic plane, with the Poincare disc model and  , then the geodesic ray from
, then the geodesic ray from  is just a straight line through the origin. The neighborhood
is just a straight line through the origin. The neighborhood  is a tube around the geodesic line which shrinks in diameter as it gets closer to the boundary, where it collapses to a single point. If we assume the function
is a tube around the geodesic line which shrinks in diameter as it gets closer to the boundary, where it collapses to a single point. If we assume the function  could be extended to the closure of the disc (which is the geodesic compactification of
could be extended to the closure of the disc (which is the geodesic compactification of  ), then we are faced with the following difficult question: What are the limit points of the set
), then we are faced with the following difficult question: What are the limit points of the set  ?
?
Clearly, this set is unbounded in the hyperbolic metric, so by compactness it would have to have some limit point on the boundary of the disk. However, these points lie in  and since
and since  collapses to a single point on the boundary, we conclude that
collapses to a single point on the boundary, we conclude that  intersects the boundary at precisely two points, namely the limit points of
intersects the boundary at precisely two points, namely the limit points of  . Thus we find that by choosing what sequence in
. Thus we find that by choosing what sequence in  converges to the boundary point of
converges to the boundary point of  , the “extension” of
, the “extension” of  can attain any value between
can attain any value between  and
and  on these boundary points. Thus the extension cannot be continuous.
on these boundary points. Thus the extension cannot be continuous.
In a slightly more general terms, let us try to create a bump like function for the collection of irregular boundary points. Recall that a point  on the geodesic boundary is called irregular if the corresponding geodesic
on the geodesic boundary is called irregular if the corresponding geodesic ![Rendered by QuickLaTeX.com [\gamma] = v](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-21ab5f5d0d5f37ae73957c6e4be11752_l3.png) is contain in at least two maximal totally geodesic submanifolds of
is contain in at least two maximal totally geodesic submanifolds of  .
.
Let  be a non-compact symmetric space, let
be a non-compact symmetric space, let  be any point. Let
be any point. Let  be the union of all geodesic rays from
be the union of all geodesic rays from 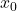 to
to  (the irregular points on the geodesic boundary). Let
(the irregular points on the geodesic boundary). Let  denote a normal neighborhood of
denote a normal neighborhood of  of radius
of radius  in the metric of
in the metric of  . This is just the union of all parallel translates of a fixed ball
. This is just the union of all parallel translates of a fixed ball  along the irregular geodesic rays from
along the irregular geodesic rays from 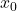 . Let
. Let ![Rendered by QuickLaTeX.com {s: X\to [0,1]}](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-e5a89abd492ad8a8d4ef6717a7fc2f73_l3.png) be a continuous bump function which is
be a continuous bump function which is  on
on  and zero outside of
and zero outside of  and assume
and assume  only depends on the distance from
only depends on the distance from  . The function
. The function  is then a bump function for the set
is then a bump function for the set  of geodesic rays from
of geodesic rays from  going towards irregular boundary points.
going towards irregular boundary points.
Let  be given by
be given by
![Rendered by QuickLaTeX.com \[\displaystyle \phi(x) = 1 - s(x)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-f1750647011def086fd31f03be7b29f6_l3.png)
The function  is clearly continuous and bounded on
is clearly continuous and bounded on  . Since it is a very natural construction, it may be interesting to look at what function we get on the boundary when we extend
. Since it is a very natural construction, it may be interesting to look at what function we get on the boundary when we extend  to certain compactifications of
to certain compactifications of  .
.
First, let us look at the the situation for the geodesic compactification. We will show the function  converges radially to a well defined function on
converges radially to a well defined function on  which is
which is  on the regular boundary points and
on the regular boundary points and  on the irregular boundary points. Though we should emphasize that the extension is radial, and not continuous. Continuous extensions cannot exist, as the next lemma shows
on the irregular boundary points. Though we should emphasize that the extension is radial, and not continuous. Continuous extensions cannot exist, as the next lemma shows
Lemma 1 Let

be any manifold with boundary

and

. Assume

extends to a function

on

in the sense that for any sequence

, with

, we have

, then

is continuous.
In summary, if  is real valued and extends to a function on
is real valued and extends to a function on  which has a jump discontinuity at
which has a jump discontinuity at  (from
(from  to
to  in
in  ), then some sequence in
), then some sequence in  converges to
converges to  . Hence the extension is not well defined at
. Hence the extension is not well defined at  .
.
However, let us show our function  converges to a well defined function on
converges to a well defined function on  but not to the whole geodesic compactification
but not to the whole geodesic compactification  . To this end let
. To this end let
![Rendered by QuickLaTeX.com \[\displaystyle U_r^n := \{ \xi \in \partial X ~|~ \xi = [\gamma], ~ \text{with } \gamma(0) = x_0, \text{ and } \gamma(n) \in U_r \}\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-f0a4c7f17d4c36ef1bf1634a7359c137_l3.png)
the shadow of  in
in  . We have –
. We have –
Lemma 2 The sets

are open neighborhoods of

and
![Rendered by QuickLaTeX.com \[\displaystyle \bigcap_{n\in \N} U_r^n = \partial X_{irr}.\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-f2c99dfb4a57933903d8390006920d88_l3.png)
Now if  is a sequence converging to
is a sequence converging to  , then, using the definition of the topology on
, then, using the definition of the topology on  , if
, if  denotes the unit vector corresponding to the geodesic ray from
denotes the unit vector corresponding to the geodesic ray from 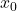 to
to  and
and  the geodesic ray going to
the geodesic ray going to  , then the
, then the  in
in  . Picking any open neighborhood
. Picking any open neighborhood  of
of  such that
such that  . Then for
. Then for  large enough we have
large enough we have  and
and  for all
for all  , where the last part follow from the above lemma. It follows that the geodesic ray converging to
, where the last part follow from the above lemma. It follows that the geodesic ray converging to  is eventually outside of
is eventually outside of  and
and  . So
. So  extends to
extends to  . Note that the sequence
. Note that the sequence  was arbitrary in the above example, so
was arbitrary in the above example, so  extends continuously to
extends continuously to  .
.
However, we cannot extend continuously to  . If
. If  , then
, then  for some
for some  . But if
. But if  this does not imply
this does not imply  . It is actually possible to check that
. It is actually possible to check that  can converge to any value in
can converge to any value in ![Rendered by QuickLaTeX.com {[0, 1]}](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-51f423ae33ef5a177613e9cf3349af30_l3.png) by converging along different sequences
by converging along different sequences  to the same irregular point. What we mean by extending
to the same irregular point. What we mean by extending  to
to  is that we extend it along geodesic rays from
is that we extend it along geodesic rays from 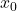 . In this case, there is only one value
. In this case, there is only one value  can attain at any point in
can attain at any point in  and we are done.
and we are done.
1. Karpelevich compactification to the rescue
The function  does however extend to a continuous function on the Karpelevich compactification
does however extend to a continuous function on the Karpelevich compactification  . Let’s see why. The book of Borel and Ji is our reference for the definitions of the Karpelevich compactification.
. Let’s see why. The book of Borel and Ji is our reference for the definitions of the Karpelevich compactification.
We will not define it here, but we will need to know that boundary points of  can be written as tuples
can be written as tuples  , where
, where  and
and  and
and  is the Karpelevich compactification of the boundary symmetric space at
is the Karpelevich compactification of the boundary symmetric space at  , meaning if
, meaning if  is the parabolic subgroup stabilizing
is the parabolic subgroup stabilizing  , then
, then
![Rendered by QuickLaTeX.com \[{X_\xi = M_\xi/(M_\xi\cap K)}.\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-46c96a73556f9b43803f833256ac676a_l3.png)
The space

can be identified with the totally geodesic submanifold

and its geodesic compactification is isomorphic to the closure of

in

. In case

has rank

the compactification

by definition. Since

has rank lower than

, if

, the boundary

can be expressed using only the geodesic compactification, which simplifies the exposition.
Assuming a sequence of points  converge to a boundary point
converge to a boundary point  . Then, one can always express
. Then, one can always express  as
as
![Rendered by QuickLaTeX.com \[\displaystyle x_i = g_i a_i m_i\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-36db5c7889f50508c5ee239b385fd75a_l3.png)
where  ,
,  is a representative in
is a representative in  and
and  are such that
are such that  (mentioned in the proof of Proposition I.15.6 of but also implicit in the definition of the Karpelevich compactification on p. 53).
(mentioned in the proof of Proposition I.15.6 of but also implicit in the definition of the Karpelevich compactification on p. 53).
The sequence  converges to
converges to  if and only if
if and only if
 in
in  or equivalently
or equivalently  in
in  .
. in
in  .
.
Now  be a sequence converging to
be a sequence converging to  where
where  and
and  (recall that we assume
(recall that we assume  has rank 2!). Let
has rank 2!). Let  be the geodesic centered at
be the geodesic centered at 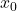 in the direction of
in the direction of  , i.e.
, i.e.  and
and  . Recall that
. Recall that  is the Cartan subgroup of
is the Cartan subgroup of  , hence
, hence  is a limit point of
is a limit point of  in
in  , and we can write
, and we can write  for some
for some  (if not we would have to write
(if not we would have to write  for some
for some  using the polar decomposition of
using the polar decomposition of  described in a previous blog post).
described in a previous blog post).

since  (so
(so  uniformly in
uniformly in  ) and
) and  is a totally geodesic submanifold of
is a totally geodesic submanifold of  orthogonal to
orthogonal to  at
at 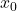 . Since
. Since  converges in the geodesic compactification of
converges in the geodesic compactification of  it follows that
it follows that  converges or diverges to
converges or diverges to  . Either way the the distance
. Either way the the distance  converges in
converges in  and if
and if  is another sequence converging to
is another sequence converging to  with
with
![Rendered by QuickLaTeX.com \[\displaystyle \lim_i d(y_i, \gamma_v) \neq \lim_i d(x_i, \gamma_v)\]](https://www.mathblog.realhjelp.no/wp-content/ql-cache/quicklatex.com-b9f451cc33a5f194de308f31b316020f_l3.png)
then  in
in  as the limit keeps track of the distance from
as the limit keeps track of the distance from  . This is all we need to ensure that
. This is all we need to ensure that  is well defined and does not depend on the choice of convergent sequence in
is well defined and does not depend on the choice of convergent sequence in  . We have thus proved
. We have thus proved
Lemma 3 The function

extends to a continuous function on the Karpelevich compactification.
Heuristically, what is happening in the Karpelevich compactificaiton is that we have taken the points on  where the function
where the function  (or
(or  ) could not be extended and “blown” them up by gluing in the boundary symmetric spaces
) could not be extended and “blown” them up by gluing in the boundary symmetric spaces  at these points. The extension of the function
at these points. The extension of the function  is then a bump function of some open set in
is then a bump function of some open set in  where
where  runs over all limit points of irregular boundary points.
runs over all limit points of irregular boundary points.
{6233257:PCE7JH8E}
apa
default
0
4592
%7B%22status%22%3A%22success%22%2C%22updateneeded%22%3Afalse%2C%22instance%22%3Afalse%2C%22meta%22%3A%7B%22request_last%22%3A0%2C%22request_next%22%3A0%2C%22used_cache%22%3Atrue%7D%2C%22data%22%3A%5B%7B%22key%22%3A%22QZ36DEMH%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Szabo%20et%20al.%22%2C%22parsedDate%22%3A%222017-03-23%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESzabo%2C%20G.%2C%20Wu%2C%20J.%2C%20%26amp%3B%20Zacharias%2C%20J.%20%282017%29.%20Rokhlin%20dimension%20for%20actions%20of%20residually%20finite%20groups.%20%3Ci%3EArXiv%3A1408.6096%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1408.6096%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1408.6096%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Rokhlin%20dimension%20for%20actions%20of%20residually%20finite%20groups%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Gabor%22%2C%22lastName%22%3A%22Szabo%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jianchao%22%2C%22lastName%22%3A%22Wu%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joachim%22%2C%22lastName%22%3A%22Zacharias%22%7D%5D%2C%22abstractNote%22%3A%22We%20introduce%20the%20concept%20of%20Rokhlin%20dimension%20for%20actions%20of%20residually%20finite%20groups%20on%20C%2A-algebras%2C%20extending%20previous%20notions%20of%20Rokhlin%20dimension%20for%20actions%20of%20finite%20groups%20and%20the%20integers%2C%20as%20introduced%20by%20Hirshberg%2C%20Winter%20and%20the%20third%20author.%20If%20the%20group%20has%20a%20box%20space%20of%20finite%20asymptotic%20dimension%2C%20then%20actions%20with%20finite%20Rokhlin%20dimension%20preserve%20the%20property%20of%20having%20finite%20nuclear%20dimension%2C%20when%20passing%20to%20the%20crossed%20product%20C%2A-algebra.%20A%20detailed%20study%20of%20the%20asymptotic%20dimension%20of%20box%20spaces%20shows%20that%20finitely%20generated%2C%20virtually%20nilpotent%20groups%20have%20box%20spaces%20with%20finite%20asymptotic%20dimension%2C%20providing%20a%20reasonably%20large%20class%20of%20examples.%20We%20then%20establish%20a%20relation%20between%20Rokhlin%20dimension%20of%20residually%20finite%20groups%20acting%20on%20compact%20metric%20spaces%20and%20amenability%20dimension%20of%20the%20action%20in%20the%20sense%20of%20Guentner%2C%20Willett%20and%20Yu.%20We%20show%20that%20for%20free%20actions%20of%20infinite%2C%20finitely%20generated%2C%20nilpotent%20groups%20on%20finite%20dimensional%20spaces%2C%20both%20these%20dimensional%20values%20are%20finite.%20In%20particular%2C%20the%20associated%20transformation%20group%20C%2A-algebras%20have%20finite%20nuclear%20dimension.%20This%20extends%20an%20analogous%20result%20about%20%24%5C%5Cmathbb%7BZ%7D%5Em%24-actions%20by%20the%20first%20author.%20We%20also%20provide%20some%20results%20concerning%20the%20genericity%20of%20finite%20Rokhlin%20dimension%2C%20and%20permanence%20properties%20with%20respect%20to%20the%20absorption%20of%20a%20strongly%20self-absorbing%20C%2A-algebra.%22%2C%22date%22%3A%222017-03-23%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1408.6096%22%2C%22collections%22%3A%5B%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-27T16%3A16%3A37Z%22%7D%7D%2C%7B%22key%22%3A%22GEN54VRQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Guentner%20et%20al.%22%2C%22parsedDate%22%3A%222015-10-27%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EGuentner%2C%20E.%2C%20Willett%2C%20R.%2C%20%26amp%3B%20Yu%2C%20G.%20%282015%29.%20Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras.%20%3Ci%3EArXiv%3A1510.07769%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Erik%22%2C%22lastName%22%3A%22Guentner%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Rufus%22%2C%22lastName%22%3A%22Willett%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Guoliang%22%2C%22lastName%22%3A%22Yu%22%7D%5D%2C%22abstractNote%22%3A%22We%20introduce%20dynamic%20asymptotic%20dimension%2C%20a%20notion%20of%20dimension%20for%20actions%20of%20discrete%20groups%20on%20locally%20compact%20spaces%2C%20and%20more%20generally%20for%20locally%20compact%20%5C%5C%27etale%20groupoids.%20We%20study%20our%20notion%20for%20minimal%20actions%20of%20the%20integer%20group%2C%20its%20relation%20with%20conditions%20used%20by%20Bartels%2C%20L%5C%5C%5C%22uck%2C%20and%20Reich%20in%20the%20context%20of%20controlled%20topology%2C%20and%20its%20connections%20with%20Gromov%27s%20theory%20of%20asymptotic%20dimension.%20We%20also%20show%20that%20dynamic%20asymptotic%20dimension%20gives%20bounds%20on%20the%20nuclear%20dimension%20of%20Winter%20and%20Zacharias%20for%20C%2A-algebras%20associated%20to%20dynamical%20systems.%20Dynamic%20asymptotic%20dimension%20also%20has%20implications%20for%20K-theory%20and%20manifold%20topology%3A%20these%20will%20be%20drawn%20out%20in%20subsequent%20work.%22%2C%22date%22%3A%222015-10-27%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%22%2C%22collections%22%3A%5B%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-27T16%3A01%3A28Z%22%7D%7D%2C%7B%22key%22%3A%226TLY87YL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Conley%20et%20al.%22%2C%22parsedDate%22%3A%222020-09-14%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EConley%2C%20C.%2C%20Jackson%2C%20S.%2C%20Marks%2C%20A.%2C%20Seward%2C%20B.%2C%20%26amp%3B%20Tucker-Drob%2C%20R.%20%282020%29.%20Borel%20asymptotic%20dimension%20and%20hyperfinite%20equivalence%20relations.%20%3Ci%3EArXiv%3A2009.06721%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2009.06721%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2009.06721%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Borel%20asymptotic%20dimension%20and%20hyperfinite%20equivalence%20relations%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Clinton%22%2C%22lastName%22%3A%22Conley%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Steve%22%2C%22lastName%22%3A%22Jackson%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Andrew%22%2C%22lastName%22%3A%22Marks%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Brandon%22%2C%22lastName%22%3A%22Seward%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robin%22%2C%22lastName%22%3A%22Tucker-Drob%22%7D%5D%2C%22abstractNote%22%3A%22A%20long%20standing%20open%20problem%20in%20the%20theory%20of%20hyperfinite%20equivalence%20relations%20asks%20if%20the%20orbit%20equivalence%20relation%20generated%20by%20a%20Borel%20action%20of%20a%20countable%20amenable%20group%20is%20hyperfinite.%20In%20this%20paper%20we%20prove%20that%20this%20question%20always%20has%20a%20positive%20answer%20when%20the%20acting%20group%20is%20polycyclic%2C%20and%20we%20obtain%20a%20positive%20answer%20for%20all%20free%20actions%20of%20a%20large%20class%20of%20solvable%20groups%20including%20the%20Baumslag--Solitar%20group%20BS%281%2C2%29%20and%20the%20lamplighter%20group.%20This%20marks%20the%20first%20time%20that%20a%20group%20of%20exponential%20volume-growth%20has%20been%20verified%20to%20have%20this%20property.%20In%20obtaining%20this%20result%20we%20introduce%20a%20new%20tool%20for%20studying%20Borel%20equivalence%20relations%20by%20extending%20Gromov%27s%20notion%20of%20asymptotic%20dimension%20to%20the%20Borel%20setting.%20We%20show%20that%20countable%20Borel%20equivalence%20relations%20of%20finite%20Borel%20asymptotic%20dimension%20are%20hyperfinite%2C%20and%20more%20generally%20we%20prove%20under%20a%20mild%20compatibility%20assumption%20that%20increasing%20unions%20of%20such%20equivalence%20relations%20are%20hyperfinite.%20As%20part%20of%20our%20main%20theorem%2C%20we%20prove%20for%20a%20large%20class%20of%20solvable%20groups%20that%20all%20of%20their%20free%20Borel%20actions%20have%20finite%20Borel%20asymptotic%20dimension%20%28and%20finite%20dynamic%20asymptotic%20dimension%20in%20the%20case%20of%20a%20continuous%20action%20on%20a%20zero-dimensional%20space%29.%20We%20also%20provide%20applications%20to%20Borel%20chromatic%20numbers%2C%20Borel%20and%20continuous%20Folner%20tilings%2C%20topological%20dynamics%2C%20and%20%24C%5E%2A%24-algebras.%22%2C%22date%22%3A%222020-09-14%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2009.06721%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%2C%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-27T15%3A53%3A30Z%22%7D%7D%2C%7B%22key%22%3A%22ZLKNIH9X%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Bell%20and%20Dranishnikov%22%2C%22parsedDate%22%3A%222007-04-03%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EBell%2C%20G.%2C%20%26amp%3B%20Dranishnikov%2C%20A.%20%282007%29.%20Asymptotic%20Dimension.%20%3Ci%3EArXiv%3AMath%5C%2F0703766%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0703766%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0703766%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Asymptotic%20Dimension%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22G.%22%2C%22lastName%22%3A%22Bell%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22A.%22%2C%22lastName%22%3A%22Dranishnikov%22%7D%5D%2C%22abstractNote%22%3A%22The%20asymptotic%20dimension%20theory%20was%20founded%20by%20Gromov%20in%20the%20early%2090s.%20In%20this%20paper%20we%20give%20a%20survey%20of%20its%20recent%20history%20where%20we%20emphasize%20two%20of%20its%20features%3A%20an%20analogy%20with%20the%20dimension%20theory%20of%20compact%20metric%20spaces%20and%20applications%20to%20the%20theory%20of%20discrete%20groups.%22%2C%22date%22%3A%222007-04-03%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0703766%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%2C%22VN6XN7ZV%22%5D%2C%22dateModified%22%3A%222021-09-21T18%3A17%3A55Z%22%7D%7D%2C%7B%22key%22%3A%227IDKA7NA%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3Edoi%3A10.1016%5C%2Fj.topol.2008.02.011%20%7C%20Elsevier%20Enhanced%20Reader%3C%5C%2Fi%3E.%20%28n.d.%29.%20https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.topol.2008.02.011%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22webpage%22%2C%22title%22%3A%22doi%3A10.1016%5C%2Fj.topol.2008.02.011%20%7C%20Elsevier%20Enhanced%20Reader%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Freader.elsevier.com%5C%2Freader%5C%2Fsd%5C%2Fpii%5C%2FS0166864108000904%3Ftoken%3D62423AC2F70087FF795AFDCB380A02B6AB4B90A905A2FC9EA3799193623E7D94EF1B01787B838446E60AA45CAEAFA7FD%26originRegion%3Deu-west-1%26originCreation%3D20210921180604%22%2C%22language%22%3A%22en%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-21T18%3A06%3A15Z%22%7D%7D%2C%7B%22key%22%3A%223AS765V2%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Guentner%20et%20al.%22%2C%22parsedDate%22%3A%222015-10-27%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EGuentner%2C%20E.%2C%20Willett%2C%20R.%2C%20%26amp%3B%20Yu%2C%20G.%20%282015%29.%20Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras.%20%3Ci%3EArXiv%3A1510.07769%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Dynamic%20Asymptotic%20Dimension%3A%20relation%20to%20dynamics%2C%20topology%2C%20coarse%20geometry%2C%20and%20%24C%5E%2A%24-algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Erik%22%2C%22lastName%22%3A%22Guentner%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Rufus%22%2C%22lastName%22%3A%22Willett%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Guoliang%22%2C%22lastName%22%3A%22Yu%22%7D%5D%2C%22abstractNote%22%3A%22We%20introduce%20dynamic%20asymptotic%20dimension%2C%20a%20notion%20of%20dimension%20for%20actions%20of%20discrete%20groups%20on%20locally%20compact%20spaces%2C%20and%20more%20generally%20for%20locally%20compact%20%5C%5C%27etale%20groupoids.%20We%20study%20our%20notion%20for%20minimal%20actions%20of%20the%20integer%20group%2C%20its%20relation%20with%20conditions%20used%20by%20Bartels%2C%20L%5C%5C%5C%22uck%2C%20and%20Reich%20in%20the%20context%20of%20controlled%20topology%2C%20and%20its%20connections%20with%20Gromov%27s%20theory%20of%20asymptotic%20dimension.%20We%20also%20show%20that%20dynamic%20asymptotic%20dimension%20gives%20bounds%20on%20the%20nuclear%20dimension%20of%20Winter%20and%20Zacharias%20for%20C%2A-algebras%20associated%20to%20dynamical%20systems.%20Dynamic%20asymptotic%20dimension%20also%20has%20implications%20for%20K-theory%20and%20manifold%20topology%3A%20these%20will%20be%20drawn%20out%20in%20subsequent%20work.%22%2C%22date%22%3A%222015-10-27%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1510.07769%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%5D%2C%22dateModified%22%3A%222021-09-21T18%3A02%3A51Z%22%7D%7D%2C%7B%22key%22%3A%22T7BM3CUF%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Serre%22%2C%22parsedDate%22%3A%221980%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESerre%2C%20J.-P.%20%281980%29.%20Trees%20and%20Amalgams.%20In%20J.-P.%20Serre%2C%20%3Ci%3ETrees%3C%5C%2Fi%3E%20%28pp.%201%26%23x2013%3B68%29.%20Springer%20Berlin%20Heidelberg.%20https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2F978-3-642-61856-7_1%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22bookSection%22%2C%22title%22%3A%22Trees%20and%20Amalgams%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22bookAuthor%22%2C%22firstName%22%3A%22Jean-Pierre%22%2C%22lastName%22%3A%22Serre%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Pierre%22%2C%22lastName%22%3A%22Serre%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22bookTitle%22%3A%22Trees%22%2C%22date%22%3A%221980%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-3-642-61858-1%20978-3-642-61856-7%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2F978-3-642-61856-7_1%22%2C%22collections%22%3A%5B%22JFPIC8ZC%22%5D%2C%22dateModified%22%3A%222021-09-21T18%3A02%3A17Z%22%7D%7D%2C%7B%22key%22%3A%225N7BHDP9%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Hill%22%2C%22parsedDate%22%3A%222021-01-16%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EHill%2C%20T.%20P.%20%282021%29.%20An%20Evolutionary%20Theory%20for%20the%20Variability%20Hypothesis.%20%3Ci%3EArXiv%3A1703.04184%20%5Bq-Bio%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1703.04184%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1703.04184%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22An%20Evolutionary%20Theory%20for%20the%20Variability%20Hypothesis%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Theodore%20P.%22%2C%22lastName%22%3A%22Hill%22%7D%5D%2C%22abstractNote%22%3A%22An%20elementary%20biostatistical%20theory%20based%20on%20a%20selectivity-variability%20principle%20is%20proposed%20to%20address%20a%20question%20raised%20by%20Charles%20Darwin%2C%20namely%2C%20how%20one%20sex%20of%20a%20sexually%20dimorphic%20species%20might%20tend%20to%20evolve%20with%20greater%20variability%20than%20the%20other%20sex.%20Briefly%2C%20the%20theory%20says%20that%20if%20one%20sex%20is%20relatively%20selective%20then%20from%20one%20generation%20to%20the%20next%2C%20more%20variable%20subpopulations%20of%20the%20opposite%20sex%20will%20generally%20tend%20to%20prevail%20over%20those%20with%20lesser%20variability.%20Moreover%2C%20the%20perhaps%20less%20intuitive%20converse%20also%20holds%3A%20if%20a%20sex%20is%20relatively%20non-selective%2C%20then%20less%20variable%20subpopulations%20of%20the%20opposite%20sex%20will%20prevail%20over%20those%20with%20greater%20variability.%20This%20theory%20requires%20certain%20regularity%20conditions%20on%20the%20distributions%2C%20but%20makes%20no%20assumptions%20about%20differences%20in%20means%20between%20the%20sexes%2C%20nor%20does%20it%20presume%20that%20one%20sex%20is%20selective%20and%20the%20other%20non-selective.%20Two%20mathematical%20models%20of%20the%20selectivity-variability%20principle%20are%20presented%3A%20a%20discrete-time%20one-step%20probabilistic%20model%20of%20short-term%20behavior%20with%20an%20example%20using%20normally%20distributed%20perceived%20fitness%20values%3B%20and%20a%20continuous-time%20deterministic%20model%20for%20the%20long-term%20asymptotic%20behavior%20of%20the%20expected%20sizes%20of%20the%20subpopulations%20with%20an%20example%20using%20exponentially%20distributed%20fitness%20levels.%22%2C%22date%22%3A%222021-01-16%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1703.04184%22%2C%22collections%22%3A%5B%2222Z435ZZ%22%5D%2C%22dateModified%22%3A%222021-09-17T15%3A43%3A34Z%22%7D%7D%2C%7B%22key%22%3A%22Z5UHF6YS%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Albuquerque%22%2C%22parsedDate%22%3A%221999-03-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EAlbuquerque%2C%20P.%20%281999%29.%20Patterson-Sullivan%20Theory%20in%20Higher%20Rank%20Symmetric%20Spaces.%20%3Ci%3EGeometric%20%26amp%3B%20Functional%20Analysis%20GAFA%3C%5C%2Fi%3E%2C%20%3Ci%3E9%3C%5C%2Fi%3E%281%29%2C%201%26%23x2013%3B28.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs000390050079%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs000390050079%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Patterson-Sullivan%20Theory%20in%20Higher%20Rank%20Symmetric%20Spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22P.%22%2C%22lastName%22%3A%22Albuquerque%22%7D%5D%2C%22abstractNote%22%3A%22Let%20X%20%3D%20G%5C%2FK%20be%20a%20Riemannian%20symmetric%20space%20of%20noncompact%20type%20and%20%24%20%5C%5CGamma%20%24a%20discrete%20%5Cu201cgeneric%5Cu201d%20subgroup%20of%20G%20with%20critical%20exponent%20%24%20%5C%5Cdelta%28%5C%5CGamma%29%20%24.%20Denote%20by%20%24%20X_%7Breg%7D%20%28%5C%5Cinfty%29%20%24the%20set%20of%20regular%20elements%20of%20the%20geometric%20boundary%20%24%20X%28%5C%5Cinfty%29%20%24of%20X.%20We%20show%20that%20the%20support%20of%20all%20%24%20%5C%5CGamma%20%24-invariant%20conformal%20densities%20of%20dimension%20%24%20%5C%5Cdelta%28%5C%5CGamma%29%20%24on%20%24%20X_%7Breg%7D%20%28%5C%5Cinfty%29%20%24%28e.g.%20Patterson-Sullivan%20densities%29%20lie%20in%20a%20same%20and%20single%20regular%20G-orbit%20on%20%24%20X%28%5C%5Cinfty%29%20%24.%20This%20provides%20information%20on%20the%20large-scale%20growth%20of%20%24%20%5C%5CGamma%20%24-orbits%20in%20X.%20If%20in%20addition%20we%20assume%20%24%20%5C%5CGamma%20%24to%20be%20of%20divergence%20type%2C%20then%20there%20is%20a%20unique%20density%20of%20the%20previous%20type.%20Furthermore%2C%20we%20explicitly%20determine%20%24%20%5C%5Cdelta%28%5C%5CGamma%29%20%24and%20this%20G-orbit%20for%20lattices%2C%20and%20show%20that%20they%20are%20of%20divergence%20type.%22%2C%22date%22%3A%221999-03-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs000390050079%22%2C%22ISSN%22%3A%221420-8970%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs000390050079%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-09-06T14%3A17%3A30Z%22%7D%7D%2C%7B%22key%22%3A%22DDWYEVQ6%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kadison%20and%20Ringrose%22%2C%22parsedDate%22%3A%221972%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281972%29.%20Cohomology%20of%20operator%20algebras.%20III%26%23x202F%3B%3A%20reduction%20to%20normal%20cohomology.%20%3Ci%3EBulletin%20de%20la%20Soci%26%23xE9%3Bt%26%23xE9%3B%20Math%26%23xE9%3Bmatique%20de%20France%3C%5C%2Fi%3E%2C%20%3Ci%3E100%3C%5C%2Fi%3E%2C%2073%26%23x2013%3B96.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras.%20III%20%3A%20reduction%20to%20normal%20cohomology%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221972%22%2C%22language%22%3A%22fr%22%2C%22DOI%22%3A%2210.24033%5C%2Fbsmf.1731%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fwww.numdam.org%5C%2Fitem%5C%2F%3Fid%3DBSMF_1972__100__73_0%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-05T14%3A23%3A08Z%22%7D%7D%2C%7B%22key%22%3A%22AFZF3PHG%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kadison%20and%20Ringrose%22%2C%22parsedDate%22%3A%221971-12%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281971%29.%20Cohomology%20of%20operator%20algebras%20II.%20Extended%20cobounding%20and%20the%20hyperfinite%20case.%20%3Ci%3EArkiv%20F%26%23xF6%3Br%20Matematik%3C%5C%2Fi%3E%2C%20%3Ci%3E9%3C%5C%2Fi%3E%281%26%23x2013%3B2%29%2C%2055%26%23x2013%3B63.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02383637%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02383637%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras%20II.%20Extended%20cobounding%20and%20the%20hyperfinite%20case%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22Arkiv%20f%5Cu00f6r%20Matematik%22%2C%22date%22%3A%221971%5C%2F12%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2FBF02383637%22%2C%22ISSN%22%3A%220004-2080%2C%201871-2487%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fprojecteuclid.org%5C%2Fjournals%5C%2Farkiv-for-matematik%5C%2Fvolume-9%5C%2Fissue-1-2%5C%2FCohomology-of-operator-algebras-II-Extended-cobounding-and-the-hyperfinite%5C%2F10.1007%5C%2FBF02383637.full%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-05T14%3A22%3A24Z%22%7D%7D%2C%7B%22key%22%3A%222SVX5YLX%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kadison%20and%20Ringrose%22%2C%22parsedDate%22%3A%221971-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281971%29.%20Cohomology%20of%20operator%20algebras%3A%20I.%20Type%20I%20von%20Neumann%20algebras.%20%3Ci%3EActa%20Mathematica%3C%5C%2Fi%3E%2C%20%3Ci%3E126%3C%5C%2Fi%3E%28none%29%2C%20227%26%23x2013%3B243.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02392032%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF02392032%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras%3A%20I.%20Type%20I%20von%20Neumann%20algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22Acta%20Mathematica%22%2C%22date%22%3A%221971%5C%2F01%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2FBF02392032%22%2C%22ISSN%22%3A%220001-5962%2C%201871-2509%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fprojecteuclid.org%5C%2Fjournals%5C%2Facta-mathematica%5C%2Fvolume-126%5C%2Fissue-none%5C%2FCohomology-of-operator-algebras--I-Type-I-von-Neumann%5C%2F10.1007%5C%2FBF02392032.full%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-05T14%3A20%3A58Z%22%7D%7D%2C%7B%22key%22%3A%22ZCEX2Z5M%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pop%20and%20Smith%22%2C%22parsedDate%22%3A%222010-04-15%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EPop%2C%20F.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%282010%29.%20Vanishing%20of%20second%20cohomology%20for%20tensor%20products%20of%20type%20II1%20von%20Neumann%20algebras.%20%3Ci%3EJournal%20of%20Functional%20Analysis%3C%5C%2Fi%3E%2C%20%3Ci%3E258%3C%5C%2Fi%3E%288%29%2C%202695%26%23x2013%3B2707.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.jfa.2010.01.013%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.jfa.2010.01.013%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Vanishing%20of%20second%20cohomology%20for%20tensor%20products%20of%20type%20II1%20von%20Neumann%20algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Florin%22%2C%22lastName%22%3A%22Pop%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22We%20show%20that%20the%20second%20cohomology%20group%20H2%28M%5Cu2297%5Cu00afN%2CM%5Cu2297%5Cu00afN%29%20is%20always%20zero%20for%20arbitrary%20type%20II1%20von%20Neumann%20algebras%20M%20and%20N.%22%2C%22date%22%3A%22April%2015%2C%202010%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.jfa.2010.01.013%22%2C%22ISSN%22%3A%220022-1236%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.sciencedirect.com%5C%2Fscience%5C%2Farticle%5C%2Fpii%5C%2FS002212361000025X%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T19%3A07%3A21Z%22%7D%7D%2C%7B%22key%22%3A%224RNRZD9Y%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Christensen%20et%20al.%22%2C%22parsedDate%22%3A%222003-09-21%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EChristensen%2C%20E.%2C%20Pop%2C%20F.%2C%20Sinclair%2C%20A.%2C%20%26amp%3B%20Smith%2C%20R.%20%282003%29.%20Hochschild%20Cohomology%20Of%20Factors%20With%20Property%20Gamma.%20%3Ci%3EAnnals%20of%20Mathematics%3C%5C%2Fi%3E%2C%20%3Ci%3E158%3C%5C%2Fi%3E%2C%20635%26%23x2013%3B659.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20Cohomology%20Of%20Factors%20With%20Property%20Gamma%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Erik%22%2C%22lastName%22%3A%22Christensen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Florin%22%2C%22lastName%22%3A%22Pop%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20main%20result%20of%20this%20paper%20is%20that%20the%20k%20th%20continuous%20Hochschild%20cohomology%20groups%20H%20k%20%28M%2CM%29%20and%20H%20k%20%28M%2CB%28H%29%29%20of%20a%20von%20Neumann%20factor%20M%20%23%20B%28H%29%20of%20type%20II%201%20with%20property%20%23%20are%20zero%20for%20all%20positive%20integers%20k.%20The%20method%20of%20proof%20involves%20the%20construction%20of%20hyperfinite%20subfactors%20with%20special%20properties%20and%20a%20new%20inequality%20of%20Grothendieck%20type%20for%20multilinear%20maps.%20We%20prove%20joint%20continuity%20in%20the%20%23%20%23%202%20-norm%20of%20separately%20ultraweakly%20continuous%20multilinear%20maps%2C%20and%20combine%20these%20results%20to%20reduce%20to%20the%20case%20of%20completely%20bounded%20cohomology%20which%20is%20already%20solved.%20%23%20Partially%20supported%20by%20a%20Scheme%204%20collaborative%20grant%20from%20the%20London%20Mathematical%20Society.%20%2B%20Partially%20supported%20by%20a%20grant%20from%20the%20National%20Science%20Foundation.%201%22%2C%22date%22%3A%22September%2021%2C%202003%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T18%3A18%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22LNLGCBPB%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3EHochschild%20cohomology%20of%20factors%20with%20property%20%24%5C%5CGamma%24%20%7C%20Annals%20of%20Mathematics%3C%5C%2Fi%3E.%20%28n.d.%29.%20Retrieved%20September%204%2C%202021%2C%20from%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fannals.math.princeton.edu%5C%2F2003%5C%2F158-2%5C%2Fp07%27%3Ehttps%3A%5C%2F%5C%2Fannals.math.princeton.edu%5C%2F2003%5C%2F158-2%5C%2Fp07%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22blogPost%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20factors%20with%20property%20%24%5C%5CGamma%24%20%7C%20Annals%20of%20Mathematics%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22blogTitle%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fannals.math.princeton.edu%5C%2F2003%5C%2F158-2%5C%2Fp07%22%2C%22language%22%3A%22en-US%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A17%3A22Z%22%7D%7D%2C%7B%22key%22%3A%224R2I4SCQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Cameron%22%2C%22parsedDate%22%3A%222009-06-01%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ECameron%2C%20J.%20%282009%29.%20Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras.%20%3Ci%3EProceedings%20of%20the%20Edinburgh%20Mathematical%20Society%3C%5C%2Fi%3E%2C%20%3Ci%3E52%3C%5C%2Fi%3E%2C%20287%26%23x2013%3B295.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jan%22%2C%22lastName%22%3A%22Cameron%22%7D%5D%2C%22abstractNote%22%3A%22In%20this%20paper%20we%20prove%20that%2C%20for%20a%20type-II1%20factor%20N%20with%20a%20Cartan%20maximal%20abelian%20subalgebra%2C%20the%20Hochschild%20cohomology%20groups%20Hn%28N%2CN%29%3D0%20for%20all%20n%5Cu22651.%20This%20generalizes%20the%20result%20of%20Sinclair%20and%20Smith%2C%20who%20proved%20this%20for%20all%20N%20having%20a%20separable%20predual.%22%2C%22date%22%3A%22June%201%2C%202009%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1017%5C%2FS0013091507000053%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T18%3A12%3A58Z%22%7D%7D%2C%7B%22key%22%3A%22AI5Z6XM6%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Cameron%22%2C%22parsedDate%22%3A%222009%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ECameron%2C%20J.%20%282009%29.%20Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras.%20%3Ci%3EProceedings%20of%20the%20Edinburgh%20Mathematical%20Society%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1017%5C%2FS0013091507000053%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20II1%20factors%20with%20Cartan%20maximal%20abelian%20subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22J.%22%2C%22lastName%22%3A%22Cameron%22%7D%5D%2C%22abstractNote%22%3A%22Abstract%20In%20this%20paper%20we%20prove%20that%2C%20for%20a%20type-II1%20factor%20N%20with%20a%20Cartan%20maximal%20abelian%20subalgebra%2C%20the%20Hochschild%20cohomology%20groups%20Hn%28N%2CN%29%3D0%20for%20all%20n%5Cu22651.%20This%20generalizes%20the%20result%20of%20Sinclair%20and%20Smith%2C%20who%20proved%20this%20for%20all%20N%20having%20a%20separable%20predual.%22%2C%22date%22%3A%222009%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1017%5C%2FS0013091507000053%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A12%3A46Z%22%7D%7D%2C%7B%22key%22%3A%223JBVWD3W%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Johnson%20et%20al.%22%2C%22parsedDate%22%3A%221972%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EJohnson%2C%20B.%20E.%2C%20Kadison%2C%20R.%20V.%2C%20%26amp%3B%20Ringrose%2C%20J.%20R.%20%281972%29.%20Cohomology%20of%20operator%20algebras.%20III%26%23x202F%3B%3A%20reduction%20to%20normal%20cohomology.%20%3Ci%3EBulletin%20de%20La%20Soci%26amp%3B%23233%3BT%26amp%3B%23233%3B%20Math%26amp%3B%23233%3BMatique%20de%20France%3C%5C%2Fi%3E%2C%20%3Ci%3E79%3C%5C%2Fi%3E%2C%2073%26%23x2013%3B96.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.24033%5C%2Fbsmf.1731%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Cohomology%20of%20operator%20algebras.%20III%20%3A%20reduction%20to%20normal%20cohomology%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22B.E.%22%2C%22lastName%22%3A%22Johnson%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%20V.%22%2C%22lastName%22%3A%22Kadison%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22John%20R.%22%2C%22lastName%22%3A%22Ringrose%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221972%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.24033%5C%2Fbsmf.1731%22%2C%22ISSN%22%3A%220037-9484%2C%202102-622X%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fwww.numdam.org%5C%2Fitem%3Fid%3DBSMF_1972__100__73_0%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A05%3A55Z%22%7D%7D%2C%7B%22key%22%3A%22DHK3YBPG%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sinclair%20and%20Smith%22%2C%22parsedDate%22%3A%221998%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESinclair%2C%20A.%20M.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%281998%29.%20Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras.%20%3Ci%3EAmerican%20Journal%20of%20Mathematics%3C%5C%2Fi%3E%2C%20%3Ci%3E120%3C%5C%2Fi%3E%285%29%2C%201043%26%23x2013%3B1057.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%27%3Ehttps%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%20M.%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20main%20result%20of%20this%20paper%20is%20that%20%24H%5E%7Bn%7D%28%7B%5C%5Ccal%20M%7D%2C%7B%5C%5Ccal%20M%7D%29%3D0%24%2C%20n%20%5Cu2265%201%2C%20for%20von%20Neumann%20algebras%20%24%7B%5C%5Ccal%20M%7D%24%20with%20Cartan%20subalgebras%20and%20separable%20preduals.%22%2C%22date%22%3A%221998%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%220002-9327%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T18%3A05%3A16Z%22%7D%7D%2C%7B%22key%22%3A%223H57X7HU%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sinclair%20and%20Smith%22%2C%22parsedDate%22%3A%221998%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESinclair%2C%20A.%20M.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%281998%29.%20Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras.%20%3Ci%3EAmerican%20Journal%20of%20Mathematics%3C%5C%2Fi%3E%2C%20%3Ci%3E120%3C%5C%2Fi%3E%285%29%2C%201043%26%23x2013%3B1057.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%27%3Ehttps%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20Cohomology%20for%20Von%20Neumann%20Algebras%20with%20Cartan%20Subalgebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%20M.%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20main%20result%20of%20this%20paper%20is%20that%20%24H%5E%7Bn%7D%28%7B%5C%5Ccal%20M%7D%2C%7B%5C%5Ccal%20M%7D%29%3D0%24%2C%20n%20%5Cu2265%201%2C%20for%20von%20Neumann%20algebras%20%24%7B%5C%5Ccal%20M%7D%24%20with%20Cartan%20subalgebras%20and%20separable%20preduals.%22%2C%22date%22%3A%221998%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%220002-9327%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.jstor.org%5C%2Fstable%5C%2F25098635%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T18%3A04%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22HQNQUFLG%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Qian%20and%20Shen%22%2C%22parsedDate%22%3A%222014-11-12%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EQian%2C%20W.%2C%20%26amp%3B%20Shen%2C%20J.%20%282014%29.%20Hochschild%20cohomology%20of%20type%20II%24_1%24%20von%20Neumann%20algebras%20with%20Property%20%24%5C%5CGamma%24.%20%3Ci%3EArXiv%3A1407.0664%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1407.0664%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1407.0664%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hochschild%20cohomology%20of%20type%20II%24_1%24%20von%20Neumann%20algebras%20with%20Property%20%24%5C%5CGamma%24%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Wenhua%22%2C%22lastName%22%3A%22Qian%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Junhao%22%2C%22lastName%22%3A%22Shen%22%7D%5D%2C%22abstractNote%22%3A%22In%20this%20paper%2C%20Property%20%24%5C%5CGamma%24%20for%20a%20type%20II%24_%7B1%7D%24%20von%20Neumann%20algebra%20is%20introduced%20as%20a%20generalization%20of%20Murray%20and%20von%20Neumann%27s%20Property%20%24%5C%5CGamma%24%20for%20a%20type%20II%24_%7B1%7D%24%20factor.%20The%20main%20result%20of%20this%20paper%20is%20that%20if%20a%20type%20II%24_%7B1%7D%24%20von%20Neumann%20algebra%20%24%5C%5Cmathcal%7BM%7D%24%20with%20separable%20predual%20has%20Property%20%24%5C%5CGamma%24%2C%20then%20the%20continuous%20Hochschild%20cohomology%20group%20%24H%5E%7Bk%7D%28%5C%5Cmathcal%7BM%7D%2C%20%5C%5Cmathcal%7BM%7D%29%24%20vanishes%20for%20every%20%24k%20%5C%5Cgeq%202%24.%20This%20gives%20a%20generalization%20of%20an%20earlier%20result%20due%20to%20E.%20Christensen%2C%20F.%20Pop%2C%20A.M.%20Sinclair%20and%20R.R.%20Smith.%22%2C%22date%22%3A%222014-11-12%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1407.0664%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T17%3A53%3A21Z%22%7D%7D%2C%7B%22key%22%3A%22T2TTP4WL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sinclair%20and%20Smith%22%2C%22parsedDate%22%3A%221995-03-09%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESinclair%2C%20A.%20M.%2C%20%26amp%3B%20Smith%2C%20R.%20R.%20%281995%29.%20%3Ci%3EHochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%3C%5C%2Fi%3E.%20Cambridge%20University%20Press.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22Hochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Allan%20M.%22%2C%22lastName%22%3A%22Sinclair%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Roger%20R.%22%2C%22lastName%22%3A%22Smith%22%7D%5D%2C%22abstractNote%22%3A%22The%20subject%20of%20this%20book%20is%20the%20continuous%20Hochschild%20cohomology%20of%20dual%20normal%20modules%20over%20a%20von%20Neumann%20algebra.%20The%20authors%20develop%20the%20necessary%20technical%20results%2C%20assuming%20a%20familiarity%20with%20basic%20C%2A-algebra%20and%20von%20Neumann%20algebra%20theory%2C%20including%20the%20decomposition%20into%20types%2C%20but%20no%20prior%20knowledge%20of%20cohomology%20theory%20is%20required%20and%20the%20theory%20of%20completely%20bounded%20and%20multilinear%20operators%20is%20given%20fully.%20Those%20cases%20when%20the%20continuous%20Hochschild%20cohomology%20Hn%28M%2CM%29%20of%20the%20von%20Neumann%20algebra%20M%20over%20itself%20is%20zero%20are%20central%20to%20this%20book.%20The%20material%20in%20this%20book%20lies%20in%20the%20area%20common%20to%20Banach%20algebras%2C%20operator%20algebras%20and%20homological%20algebra%2C%20and%20will%20be%20of%20interest%20to%20researchers%20from%20these%20fields.%22%2C%22date%22%3A%221995-03-09%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-0-521-47880-9%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22T97BP4CA%22%5D%2C%22dateModified%22%3A%222021-09-04T17%3A51%3A20Z%22%7D%7D%2C%7B%22key%22%3A%228QR33GYL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3EHochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%20%7C%20Abstract%20analysis%3C%5C%2Fi%3E.%20%28n.d.%29.%20Cambridge%20University%20Press.%20Retrieved%20September%204%2C%202021%2C%20from%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%5C%2Fhochschild-cohomology-von-neumann-algebras%2C%20https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%27%3Ehttps%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%5C%2Fhochschild-cohomology-von-neumann-algebras%2C%20https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22webpage%22%2C%22title%22%3A%22Hochschild%20Cohomology%20of%20Von%20Neumann%20Algebras%20%7C%20Abstract%20analysis%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%5C%2Fhochschild-cohomology-von-neumann-algebras%2C%20https%3A%5C%2F%5C%2Fwww.cambridge.org%5C%2Fit%5C%2Facademic%5C%2Fsubjects%5C%2Fmathematics%5C%2Fabstract-analysis%22%2C%22language%22%3A%22en%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-09-04T17%3A50%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22H3AX2L9L%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Eynard%22%2C%22parsedDate%22%3A%222014-12-12%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EEynard%2C%20B.%20%282014%29.%20A%20short%20overview%20of%20the%20%26%23x201C%3BTopological%20recursion.%26%23x201D%3B%20%3Ci%3EArXiv%3A1412.3286%20%5BHep-Th%2C%20Physics%3AMath-Ph%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1412.3286%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1412.3286%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20short%20overview%20of%20the%20%5C%22Topological%20recursion%5C%22%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22B.%22%2C%22lastName%22%3A%22Eynard%22%7D%5D%2C%22abstractNote%22%3A%22This%20review%20is%20an%20extended%20version%20of%20the%20Seoul%20ICM%202014%20proceedings.It%20is%20a%20short%20overview%20of%20the%20%5C%22topological%20recursion%5C%22%2C%20a%20relation%20appearing%20in%20the%20asymptotic%20expansion%20of%20many%20integrable%20systems%20and%20in%20enumerative%20problems.%20We%20recall%20how%20computing%20large%20size%20asymptotics%20in%20random%20matrices%2C%20has%20allowed%20to%20discover%20some%20fascinating%20and%20ubiquitous%20geometric%20invariants.%20Specializations%20of%20this%20method%20recover%20many%20classical%20invariants%2C%20like%20Gromov--Witten%20invariants%2C%20or%20knot%20polynomials%20%28Jones%2C%20HOMFLY%2C...%29.%20In%20this%20short%20review%2C%20we%20give%20some%20examples%2C%20give%20definitions%2C%20and%20review%20some%20properties%20and%20applications%20of%20the%20formalism.%22%2C%22date%22%3A%222014-12-12%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1412.3286%22%2C%22collections%22%3A%5B%22DX5YKRMR%22%5D%2C%22dateModified%22%3A%222021-09-02T14%3A23%3A02Z%22%7D%7D%2C%7B%22key%22%3A%22RD8GIFC3%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pimsner%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EPimsner%2C%20M.%20V.%20%281986%29.%20KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees.%20%3Ci%3EInventiones%20Mathematicae%3C%5C%2Fi%3E%2C%20%3Ci%3E86%3C%5C%2Fi%3E%283%29%2C%20603%26%23x2013%3B634.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Mihai%20V.%22%2C%22lastName%22%3A%22Pimsner%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2210%5C%2F1986%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2FBF01389271%22%2C%22ISSN%22%3A%220020-9910%2C%201432-1297%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2FBF01389271%22%2C%22collections%22%3A%5B%22K674WRBB%22%5D%2C%22dateModified%22%3A%222021-08-27T13%3A20%3A23Z%22%7D%7D%2C%7B%22key%22%3A%22I924RBCP%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pimsner%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EPimsner%2C%20M.%20%281986%29.%20%3Ci%3EKK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2FBF01389271%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22M.%22%2C%22lastName%22%3A%22Pimsner%22%7D%5D%2C%22abstractNote%22%3A%22Semantic%20Scholar%20extracted%20view%20of%20%5C%22KK-groups%20of%20crossed%20products%20by%20groups%20acting%20on%20trees%5C%22%20by%20M.%20Pimsner%22%2C%22date%22%3A%221986%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2FBF01389271%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22K674WRBB%22%5D%2C%22dateModified%22%3A%222021-08-27T13%3A19%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22A2CAVRNJ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Rieffel%22%2C%22parsedDate%22%3A%221982%22%2C%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ERieffel%2C%20M.%20%281982%29.%20%3Ci%3EApplications%20of%20strong%20Morita%20equivalence%20for%20transofrmation%20C%2A-algebras%3C%5C%2Fi%3E.%20%3Ci%3E38%3C%5C%2Fi%3E%281%29.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fmath.berkeley.edu%5C%2F~rieffel%5C%2Fpapers%5C%2Fapplications.pdf%27%3Ehttps%3A%5C%2F%5C%2Fmath.berkeley.edu%5C%2F~rieffel%5C%2Fpapers%5C%2Fapplications.pdf%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Applications%20of%20strong%20Morita%20equivalence%20for%20transofrmation%20C%2A-algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Marc%22%2C%22lastName%22%3A%22Rieffel%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221982%22%2C%22language%22%3A%22English%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fmath.berkeley.edu%5C%2F~rieffel%5C%2Fpapers%5C%2Fapplications.pdf%22%2C%22collections%22%3A%5B%22EIKGB5RV%22%2C%222AUGUVBU%22%5D%2C%22dateModified%22%3A%222021-08-27T13%3A10%3A02Z%22%7D%7D%2C%7B%22key%22%3A%222KMKAXHS%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Kloeckner%22%2C%22parsedDate%22%3A%222010%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EKloeckner%2C%20B.%20%282010%29.%20Symmetric%20spaces%20of%20higher%20rank%20do%20not%20admit%20differentiable%20compactifications.%20%3Ci%3EMathematische%20Annalen%3C%5C%2Fi%3E%2C%20%3Ci%3E347%3C%5C%2Fi%3E%284%29%2C%20951%26%23x2013%3B961.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-009-0464-z%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-009-0464-z%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Symmetric%20spaces%20of%20higher%20rank%20do%20not%20admit%20differentiable%20compactifications%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Benoit%22%2C%22lastName%22%3A%22Kloeckner%22%7D%5D%2C%22abstractNote%22%3A%22Any%20nonpositively%20curved%20symmetric%20space%20admits%20a%20topological%20compactification%2C%20namely%20the%20Hadamard%20compactification.%20For%20rank%20one%20spaces%2C%20this%20topological%20compactification%20can%20be%20endowed%20with%20a%20differentiable%20structure%20such%20that%20the%20action%20of%20the%20isometry%20group%20is%20differentiable.%20Moreover%2C%20the%20restriction%20of%20the%20action%20on%20the%20boundary%20leads%20to%20a%20flat%20model%20for%20some%20geometry%20%28conformal%2C%20CR%20or%20quaternionic%20CR%20depending%20of%20the%20space%29.%20One%20can%20ask%20whether%20such%20a%20differentiable%20compactification%20exists%20for%20higher%20rank%20spaces%2C%20hopefully%20leading%20to%20some%20knew%20geometry%20to%20explore.%20In%20this%20paper%20we%20answer%20negatively.%22%2C%22date%22%3A%228%5C%2F2010%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2Fs00208-009-0464-z%22%2C%22ISSN%22%3A%220025-5831%2C%201432-1807%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F0912.0814%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-25T16%3A16%3A24Z%22%7D%7D%2C%7B%22key%22%3A%22SHPJMPC8%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Paradan%22%2C%22parsedDate%22%3A%222009%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EParadan%2C%20P.-E.%20%282009%29.%20Symmetric%20spaces%20of%20the%20non-compact%20type%3A%20Lie%20groups.%20%3Ci%3ES%26%23xE9%3Bminaires%20et%20Congr%26%23xE8%3Bs%3C%5C%2Fi%3E%2C%20%3Ci%3EG%26%23xE9%3Bom%26%23xE9%3Btries%20%26%23xE0%3B%20courbure%20n%26%23xE9%3Bgative%20ou%20nulle%2C%20groupes%20discrets%20et%20rigidit%26%23xE9%3Bs%3C%5C%2Fi%3E%2818%29%2C%2039%26%23x2013%3B76.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00773255%27%3Ehttps%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00773255%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Symmetric%20spaces%20of%20the%20non-compact%20type%3A%20Lie%20groups%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Paul-Emile%22%2C%22lastName%22%3A%22Paradan%22%7D%5D%2C%22abstractNote%22%3A%22In%20these%20notes%2C%20we%20give%20first%20a%20brief%20account%20to%20the%20theory%20of%20Lie%20groups.%20Then%20we%20consider%20the%20case%20of%20a%20smooth%20manifold%20with%20a%20Lie%20group%20of%20symmetries.%20When%20the%20Lie%20group%20acts%20transitively%20%28e.g.%20the%20manifold%20is%20homogeneous%29%2C%20we%20study%20the%20%28affine%29%20invariant%20connections%20on%20it.%20We%20end%20up%20with%20the%20particuler%20case%20of%20homogeneous%20spaces%20which%20are%20the%20symmetric%20spaces%20of%20the%20non-compact%20type.%22%2C%22date%22%3A%222009%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00773255%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-25T16%3A10%3A49Z%22%7D%7D%2C%7B%22key%22%3A%2256Z6HFVV%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Connes%20and%20Skandalis%22%2C%22parsedDate%22%3A%221984-12-31%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EConnes%2C%20A.%2C%20%26amp%3B%20Skandalis%2C%20G.%20%281984%29.%20The%20Longitudinal%20Index%20Theorem%20for%20Foliations.%20%3Ci%3EPublications%20of%20the%20Research%20Institute%20for%20Mathematical%20Sciences%3C%5C%2Fi%3E%2C%20%3Ci%3E20%3C%5C%2Fi%3E%286%29%2C%201139%26%23x2013%3B1183.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2977%5C%2Fprims%5C%2F1195180375%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2977%5C%2Fprims%5C%2F1195180375%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20Longitudinal%20Index%20Theorem%20for%20Foliations%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alain%22%2C%22lastName%22%3A%22Connes%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Georges%22%2C%22lastName%22%3A%22Skandalis%22%7D%5D%2C%22abstractNote%22%3A%22%7C%20published%20in%20Publications%20of%20the%20Research%20Institute%20for%20Mathematical%20Sciences%22%2C%22date%22%3A%221984%5C%2F12%5C%2F31%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.2977%5C%2Fprims%5C%2F1195180375%22%2C%22ISSN%22%3A%220034-5318%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fems.press%5C%2Fjournals%5C%2Fprims%5C%2Farticles%5C%2F3203%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%2C%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-08-25T13%3A55%3A09Z%22%7D%7D%2C%7B%22key%22%3A%22FN5G4KSP%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Schroeder%22%2C%22parsedDate%22%3A%222010-12-06%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESchroeder%2C%20M.%20%282010%29.%20Patterson-Sullivan%20distributions%20for%20symmetric%20spaces%20of%20the%20noncompact%20type.%20%3Ci%3EArXiv%3A1012.1113%20%5BMath%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1012.1113%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1012.1113%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Patterson-Sullivan%20distributions%20for%20symmetric%20spaces%20of%20the%20noncompact%20type%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Michael%22%2C%22lastName%22%3A%22Schroeder%22%7D%5D%2C%22abstractNote%22%3A%22We%20generalize%20parts%20of%20a%20special%20non-Euclidean%20calculus%20of%20pseudodifferential%20operators%2C%20which%20was%20invented%20by%20S.%20Zelditch%20for%20hyperbolic%20surfaces%2C%20to%20symmetric%20spaces%20%24X%3DG%5C%2FK%24%20of%20the%20noncompact%20type%20and%20their%20compact%20quotients%20%24Y%3D%5C%5CGamma%5C%5Cbackslash%20G%5C%2FK%24.%20We%20sometimes%20restrict%20our%20results%20to%20the%20case%20of%20rank%20one%20symmetric%20spcaes.%20The%20non-Euclidean%20setting%20extends%20the%20defintion%20of%20so-called%20Patterson-Sullivan%20distributions%2C%20which%20were%20first%20defined%20by%20N.%20Anantharaman%20and%20S.%20Zelditch%20for%20hyperbolic%20systems%2C%20in%20a%20natural%20way%20to%20arbitrary%20symmetric%20spaces%20of%20the%20noncompact%20type.%20We%20find%20an%20explicit%20intertwining%20operator%20mapping%20Patterson-Sullivan%20distributions%20into%20Wigner%20distributions.%20We%20study%20the%20important%20invariance%20and%20equivariance%20properties%20of%20these%20distributions.%20Finally%2C%20we%20describe%20asymptotic%20properties%20of%20these%20distributions.%22%2C%22date%22%3A%222010-12-06%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F1012.1113%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-20T10%3A02%3A02Z%22%7D%7D%2C%7B%22key%22%3A%2222BQI6XJ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Helgason%22%2C%22parsedDate%22%3A%221979-02-09%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EHelgason%2C%20S.%20%281979%29.%20%3Ci%3EDifferential%20Geometry%2C%20Lie%20Groups%2C%20and%20Symmetric%20Spaces%3C%5C%2Fi%3E.%20Academic%20Press.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22Differential%20Geometry%2C%20Lie%20Groups%2C%20and%20Symmetric%20Spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sigurdur%22%2C%22lastName%22%3A%22Helgason%22%7D%5D%2C%22abstractNote%22%3A%22The%20present%20book%20is%20intended%20as%20a%20textbook%20and%20reference%20work%20on%20three%20topics%20in%20the%20title.%20Together%20with%20a%20volume%20in%20progress%20on%20%5C%22Groups%20and%20Geometric%20Analysis%5C%22%20it%20supersedes%20my%20%5C%22Differential%20Geometry%20and%20Symmetric%20Spaces%2C%5C%22%20published%20in%201962.%20Since%20that%20time%20several%20branches%20of%20the%20subject%2C%20particularly%20the%20function%20theory%20on%20symmetric%20spaces%2C%20have%20developed%20substantially.%20I%20felt%20that%20an%20expanded%20treatment%20might%20now%20be%20useful.%22%2C%22date%22%3A%221979-02-09%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-0-08-087396-1%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22WNJPFJYS%22%5D%2C%22dateModified%22%3A%222021-08-20T09%3A53%3A20Z%22%7D%7D%2C%7B%22key%22%3A%22VRQJE2KE%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Emerson%20and%20Meyer%22%2C%22parsedDate%22%3A%222006%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EEmerson%2C%20H.%2C%20%26amp%3B%20Meyer%2C%20R.%20%282006%29.%20Euler%20characteristics%20and%20Gysin%20sequences%20for%20group%20actions%20on%20boundaries.%20%3Ci%3EMathematische%20Annalen%3C%5C%2Fi%3E%2C%20%3Ci%3E334%3C%5C%2Fi%3E%284%29%2C%20853%26%23x2013%3B904.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-005-0747-y%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00208-005-0747-y%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Euler%20characteristics%20and%20Gysin%20sequences%20for%20group%20actions%20on%20boundaries%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Heath%22%2C%22lastName%22%3A%22Emerson%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ralf%22%2C%22lastName%22%3A%22Meyer%22%7D%5D%2C%22abstractNote%22%3A%22Let%20G%20be%20a%20locally%20compact%20group%2C%20let%20X%20be%20a%20universal%20proper%20G-space%2C%20and%20let%20Z%20be%20a%20G-equivariant%20compactification%20of%20X%20that%20is%20H-equivariantly%20contractible%20for%20each%20compact%20subgroup%20H%20of%20G.%20Let%20W%20be%20the%20resulting%20boundary.%20Assuming%20the%20Baum-Connes%20conjecture%20for%20G%20with%20coefficients%20C%20and%20C%28W%29%2C%20we%20construct%20an%20exact%20sequence%20that%20computes%20the%20map%20on%20K-theory%20induced%20by%20the%20embedding%20of%20the%20reduced%20group%20C%2A-algebra%20of%20G%20into%20the%20crossed%20product%20of%20G%20by%20C%28W%29.%20This%20exact%20sequence%20involves%20the%20equivariant%20Euler%20characteristic%20of%20X%2C%20which%20we%20study%20using%20an%20abstract%20notion%20of%20Poincare%20duality%20in%20bivariant%20K-theory.%20As%20a%20consequence%2C%20if%20G%20is%20torsion-free%20and%20the%20Euler%20characteristic%20of%20the%20orbit%20space%20X%5C%2FG%20is%20non-zero%2C%20then%20the%20unit%20element%20of%20the%20boundary%20crossed%20product%20is%20a%20torsion%20element%20whose%20order%20is%20equal%20to%20the%20absolute%20value%20of%20the%20Euler%20characteristic%20of%20X%5C%2FG.%20Furthermore%2C%20we%20get%20a%20new%20proof%20of%20a%20theorem%20of%20Lueck%20and%20Rosenberg%20concerning%20the%20class%20of%20the%20de%20Rham%20operator%20in%20equivariant%20K-homology.%22%2C%22date%22%3A%224%5C%2F2006%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1007%5C%2Fs00208-005-0747-y%22%2C%22ISSN%22%3A%220025-5831%2C%201432-1807%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2Fmath%5C%2F0505050%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A44%3A27Z%22%7D%7D%2C%7B%22key%22%3A%22TMAT2AZQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Blackadar%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EBlackadar%2C%20B.%20%281986%29.%20%3Ci%3EK-Theory%20for%20Operator%20Algebras%3C%5C%2Fi%3E.%20Springer-Verlag.%20https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2F978-1-4613-9572-0%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22K-Theory%20for%20Operator%20Algebras%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Bruce%22%2C%22lastName%22%3A%22Blackadar%22%7D%5D%2C%22abstractNote%22%3A%22K%20-Theory%20has%20revolutionized%20the%20study%20of%20operator%20algebras%20in%20the%20last%20few%20years.%20As%20the%20primary%20component%20of%20the%20subject%20of%20%5C%22noncommutative%20topol%5Cu00ad%20ogy%2C%5C%22%20K%20-theory%20has%20opened%20vast%20new%20vistas%20within%20the%20structure%20theory%20of%20C%2A%5Cu00ad%20algebras%2C%20as%20well%20as%20leading%20to%20profound%20and%20unexpected%20applications%20of%20opera%5Cu00ad%20tor%20algebras%20to%20problems%20in%20geometry%20and%20topology.%20As%20a%20result%2C%20many%20topolo%5Cu00ad%20gists%20and%20operator%20algebraists%20have%20feverishly%20begun%20trying%20to%20learn%20each%20others%27%20subjects%2C%20and%20it%20appears%20certain%20that%20these%20two%20branches%20of%20mathematics%20have%20become%20deeply%20and%20permanently%20intertwined.%20Despite%20the%20fact%20that%20the%20whole%20subject%20is%20only%20about%20a%20decade%20old%2C%20operator%20K%20-theory%20has%20now%20reached%20a%20state%20of%20relative%20stability.%20While%20there%20will%20undoubtedly%20be%20many%20more%20revolutionary%20developments%20and%20applications%20in%20the%20future%2C%20it%20appears%20the%20basic%20theory%20has%20more%20or%20less%20reached%20a%20%5C%22final%20form.%5C%22%20But%20because%20of%20the%20newness%20of%20the%20theory%2C%20there%20has%20so%20far%20been%20no%20comprehensive%20treatment%20of%20the%20subject.%20It%20is%20the%20ambitious%20goal%20of%20these%20notes%20to%20fill%20this%20gap.%20We%20will%20develop%20the%20K%20-theory%20of%20Banach%20algebras%2C%20the%20theory%20of%20extensions%20of%20C%2A-algebras%2C%20and%20the%20operator%20K%20-theory%20of%20Kasparov%20from%20scratch%20to%20its%20most%20advanced%20aspects.%20We%20will%20not%20treat%20applications%20in%20detail%3B%20however%2C%20we%20will%20outline%20the%20most%20striking%20of%20the%20applications%20to%20date%20in%20a%20section%20at%20the%20end%2C%20as%20well%20as%20mentioning%20others%20at%20suitable%20points%20in%20the%20text.%22%2C%22date%22%3A%221986%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-1-4613-9574-4%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.springer.com%5C%2Fgp%5C%2Fbook%5C%2F9781461395744%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%2C%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A42%3A29Z%22%7D%7D%2C%7B%22key%22%3A%22NT438QC5%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ji%20and%20Macpherson%22%2C%22parsedDate%22%3A%222002%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EJi%2C%20L.%2C%20%26amp%3B%20Macpherson%2C%20R.%20%282002%29.%20Geometry%20of%20compactifications%20of%20locally%20symmetric%20spaces.%20%3Ci%3EAnnales%20de%20l%26%23x2019%3Binstitut%20Fourier%3C%5C%2Fi%3E%2C%20%3Ci%3E52%3C%5C%2Fi%3E%282%29%2C%20457%26%23x2013%3B559.%20%3Ca%20class%3D%27zp-DOIURL%27%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5802%5C%2Faif.1893%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5802%5C%2Faif.1893%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Geometry%20of%20compactifications%20of%20locally%20symmetric%20spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lizhen%22%2C%22lastName%22%3A%22Ji%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%22%2C%22lastName%22%3A%22Macpherson%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222002%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.5802%5C%2Faif.1893%22%2C%22ISSN%22%3A%220373-0956%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Faif.centre-mersenne.org%5C%2Fitem%5C%2FAIF_2002__52_2_457_0%5C%2F%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%2C%22ATJ7BNSA%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A38%3A11Z%22%7D%7D%2C%7B%22key%22%3A%2242JKA9XK%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A3%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3ENote%20series%3C%5C%2Fi%3E.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22document%22%2C%22title%22%3A%22Note%20series%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A37%3A28Z%22%7D%7D%2C%7B%22key%22%3A%22KYNUWHLL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22parsedDate%22%3A%222021%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%282021%29.%20%3Ci%3EThe%20Karpelevic%20compactification%3C%5C%2Fi%3E.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22document%22%2C%22title%22%3A%22The%20Karpelevic%20compactification%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222021%22%2C%22language%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22DNMEBDYE%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A36%3A17Z%22%7D%7D%2C%7B%22key%22%3A%2246VA6ZKL%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A0%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%28N.d.%29.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22%22%2C%22ISBN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-08-01T17%3A32%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22ZSHTDFU3%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Jin%22%2C%22parsedDate%22%3A%222021-07-28%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EJin%2C%20X.%20%282021%29.%20Homological%20Mirror%20Symmetry%20for%20the%20universal%20centralizers%20I%3A%20The%20adjoint%20group%20case.%20%3Ci%3EArXiv%3A2107.13395%20%5BMath-Ph%5D%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2107.13395%27%3Ehttp%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2107.13395%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Homological%20Mirror%20Symmetry%20for%20the%20universal%20centralizers%20I%3A%20The%20adjoint%20group%20case%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Xin%22%2C%22lastName%22%3A%22Jin%22%7D%5D%2C%22abstractNote%22%3A%22We%20prove%20homological%20mirror%20symmetry%20for%20the%20universal%20centralizer%20%24J_G%24%20%28a.k.a%20Toda%20space%29%2C%20associated%20to%20any%20complex%20semisimple%20Lie%20group%20%24G%24.%20The%20A-side%20is%20a%20partially%20wrapped%20Fukaya%20category%20on%20%24J_G%24%2C%20and%20the%20B-side%20is%20the%20category%20of%20coherent%20sheaves%20on%20the%20categorical%20quotient%20of%20a%20dual%20maximal%20torus%20by%20the%20Weyl%20group%20action%20%28with%20some%20modification%20if%20%24G%24%20has%20a%20nontrivial%20center%29.%20This%20is%20the%20first%20and%20the%20main%20part%20of%20a%20two-part%20series%2C%20dealing%20with%20%24G%24%20of%20adjoint%20type.%20The%20general%20case%20will%20be%20proved%20in%20the%20forthcoming%20second%20part%20%5BJin2%5D.%22%2C%22date%22%3A%222021-07-28%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Farxiv.org%5C%2Fabs%5C%2F2107.13395%22%2C%22collections%22%3A%5B%22WNJPFJYS%22%5D%2C%22dateModified%22%3A%222021-07-30T13%3A12%3A13Z%22%7D%7D%2C%7B%22key%22%3A%22JUAPTIL6%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Soule%22%2C%22parsedDate%22%3A%222004-03%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESoule%2C%20C.%20%282004%29.%20%3Ci%3EAn%20introduction%20to%20arithmetic%20groups%3C%5C%2Fi%3E.%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00001348%27%3Ehttps%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00001348%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22manuscript%22%2C%22title%22%3A%22An%20introduction%20to%20arithmetic%20groups%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Christophe%22%2C%22lastName%22%3A%22Soule%22%7D%5D%2C%22abstractNote%22%3A%22Arithmetic%20groups%20are%20groups%20of%20matrices%20with%20integral%20entries.We%20shall%20first%20discuss%20their%20origin%20in%20number%20theory%20%28Gauss%2C%20Minkowski%29and%20their%20role%20in%20the%20%5C%22reduction%20theory%20of%20quadratic%20forms%5C%22.Then%20we%20shall%20describe%20these%20groups%20by%20generators%20and%20relations.The%20next%20topic%20will%20be%3A%20are%20all%20subgroups%20of%20finite%20indexgiven%20by%20congruence%20conditions%3F%20Finally%2C%20we%20shall%20discuss%20rigidityproperties%20of%20arithmetic%20groups.%22%2C%22manuscriptType%22%3A%22%22%2C%22date%22%3A%22March%202004%22%2C%22language%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fhal.archives-ouvertes.fr%5C%2Fhal-00001348%22%2C%22collections%22%3A%5B%22GBBXXUW9%22%5D%2C%22dateModified%22%3A%222021-06-29T13%3A05%3A15Z%22%7D%7D%2C%7B%22key%22%3A%222II5QJSK%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Rosenberg%20and%20Schochet%22%2C%22parsedDate%22%3A%221986%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ERosenberg%2C%20J.%20M.%2C%20%26amp%3B%20Schochet%2C%20C.%20%281986%29.%20%3Ci%3EThe%20K%26%23xFC%3Bnneth%20theorem%20and%20the%20universal%20coefficient%20theorem%20for%20equivariant%20K-theory%20and%20KK-theory%3C%5C%2Fi%3E.%20American%20Mathematical%20Society.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22The%20K%5Cu00fcnneth%20theorem%20and%20the%20universal%20coefficient%20theorem%20for%20equivariant%20K-theory%20and%20KK-theory%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%20M.%22%2C%22lastName%22%3A%22Rosenberg%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Claude%22%2C%22lastName%22%3A%22Schochet%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221986%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-0-8218-2349-1%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22EIKGB5RV%22%5D%2C%22dateModified%22%3A%222021-06-29T12%3A45%3A39Z%22%7D%7D%2C%7B%22key%22%3A%22G3RECNDH%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Rieffel%22%2C%22parsedDate%22%3A%222002%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ERieffel%2C%20M.%20A.%20%282002%29.%20Group%20C%26%23x2217%3B-Algebras%20as%20Compact%20Quantum%20Metric%20Spaces.%20%3Ci%3EDocumenta%20Mathematica%3C%5C%2Fi%3E%2C%2048.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Group%20C%5Cu2217-Algebras%20as%20Compact%20Quantum%20Metric%20Spaces%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Marc%20A%22%2C%22lastName%22%3A%22Rieffel%22%7D%5D%2C%22abstractNote%22%3A%22Let%20be%20a%20length%20function%20on%20a%20group%20G%2C%20and%20let%20M%20denote%20the%20operator%20of%20pointwise%20multiplication%20by%20on%202%28G%29.%20Following%20Connes%2C%20M%20can%20be%20used%20as%20a%20%5Cu201cDirac%5Cu201d%20operator%20for%20Cr%5Cu2217%28G%29.%20It%20de%5Cufb01nes%20a%20Lipschitz%20seminorm%20on%20Cr%5Cu2217%28G%29%2C%20which%20de%5Cufb01nes%20a%20metric%20on%20the%20state%20space%20of%20Cr%5Cu2217%28G%29.%20We%20investigate%20whether%20the%20topology%20from%20this%20metric%20coincides%20with%20the%20weak-%5Cu2217%20topology%20%28our%20de%5Cufb01nition%20of%20a%20%5Cu201ccompact%20quantum%20metric%20space%5Cu201d%29.%20We%20give%20an%20a%5Cufb03rmative%20answer%20for%20G%20%3D%20Zd%20when%20is%20a%20word-length%2C%20or%20the%20restriction%20to%20Zd%20of%20a%20norm%20on%20Rd.%20This%20works%20for%20Cr%5Cu2217%28G%29%20twisted%20by%20a%202-cocycle%2C%20and%20thus%20for%20noncommutative%20tori.%20Our%20approach%20involves%20Connes%5Cu2019%20cosphere%20algebra%2C%20and%20an%20interesting%20compacti%5Cufb01cation%20of%20metric%20spaces%20which%20is%20closely%20related%20to%20geodesic%20rays.%22%2C%22date%22%3A%222002%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22FHEYZTAY%22%2C%22ATJ7BNSA%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A33%3A30Z%22%7D%7D%2C%7B%22key%22%3A%22CUCW4QLQ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20Compactifications%20of%20symmetric%20spaces%20and%20their%20applications.%20%3Ci%3EX%20.%3C%5C%2Fi%3E%2C%2052.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Compactifications%20of%20symmetric%20spaces%20and%20their%20applications%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%224CDSADIM%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A28%3A54Z%22%7D%7D%2C%7B%22key%22%3A%22BDAWEY5Q%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3EAn%20example%20of%20the%20index%20of%20a%20Rockland%20operator%20on%20a%20contact%20manifold%3C%5C%2Fi%3E.%2068.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22An%20example%20of%20the%20index%20of%20a%20Rockland%20operator%20on%20a%20contact%20manifold%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%224CDSADIM%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A27%3A46Z%22%7D%7D%2C%7B%22key%22%3A%22P9CQSSC9%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3EA%20simple%20proof%20of%20the%20Hard%20Lefschetz%20theorem%3C%5C%2Fi%3E.%2037.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20simple%20proof%20of%20the%20Hard%20Lefschetz%20theorem%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%224CDSADIM%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A25%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22HRD52D7X%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ulsnaes%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EUlsnaes%2C%20T.%20%28n.d.%29.%20%3Ci%3EPensum%20MATH4450%20Videreg%26%23x2DA%3Baende%20Funksjonal%20analyse%20V%26%23x2DA%3Bar%202017%3C%5C%2Fi%3E.%2022.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Pensum%20MATH4450%20Videreg%5Cu02daaende%20Funksjonal%20analyse%20V%5Cu02daar%202017%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Torstein%22%2C%22lastName%22%3A%22Ulsnaes%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22no%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22KVPR5BHZ%22%5D%2C%22dateModified%22%3A%222021-06-22T15%3A01%3A56Z%22%7D%7D%2C%7B%22key%22%3A%22CG5RATGZ%22%2C%22library%22%3A%7B%22id%22%3A6233257%7D%2C%22meta%22%3A%7B%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%3Ci%3EVidereg%26%23xE5%3Bende%20Funksjonalanalyse%3C%5C%2Fi%3E.%20%28n.d.%29.%20Retrieved%20June%2022%2C%202021%2C%20from%20%3Ca%20class%3D%27zp-ItemURL%27%20href%3D%27https%3A%5C%2F%5C%2Fwww.overleaf.com%5C%2Fproject%5C%2F59920ace6080cd3eb133870e%27%3Ehttps%3A%5C%2F%5C%2Fwww.overleaf.com%5C%2Fproject%5C%2F59920ace6080cd3eb133870e%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22webpage%22%2C%22title%22%3A%22Videreg%5Cu00e5ende%20Funksjonalanalyse%22%2C%22creators%22%3A%5B%5D%2C%22abstractNote%22%3A%22An%20online%20LaTeX%20editor%20that%27s%20easy%20to%20use.%20No%20installation%2C%20real-time%20collaboration%2C%20version%20control%2C%20hundreds%20of%20LaTeX%20templates%2C%20and%20more.%22%2C%22date%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.overleaf.com%5C%2Fproject%5C%2F59920ace6080cd3eb133870e%22%2C%22language%22%3A%22en%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222021-06-22T15%3A00%3A49Z%22%7D%7D%5D%7D
Szabo, G., Wu, J., & Zacharias, J. (2017). Rokhlin dimension for actions of residually finite groups.
ArXiv:1408.6096 [Math].
http://arxiv.org/abs/1408.6096
Guentner, E., Willett, R., & Yu, G. (2015). Dynamic Asymptotic Dimension: relation to dynamics, topology, coarse geometry, and $C^*$-algebras.
ArXiv:1510.07769 [Math].
http://arxiv.org/abs/1510.07769
Conley, C., Jackson, S., Marks, A., Seward, B., & Tucker-Drob, R. (2020). Borel asymptotic dimension and hyperfinite equivalence relations.
ArXiv:2009.06721 [Math].
http://arxiv.org/abs/2009.06721
Bell, G., & Dranishnikov, A. (2007). Asymptotic Dimension.
ArXiv:Math/0703766.
http://arxiv.org/abs/math/0703766
doi:10.1016/j.topol.2008.02.011 | Elsevier Enhanced Reader. (n.d.). https://doi.org/10.1016/j.topol.2008.02.011
Guentner, E., Willett, R., & Yu, G. (2015). Dynamic Asymptotic Dimension: relation to dynamics, topology, coarse geometry, and $C^*$-algebras.
ArXiv:1510.07769 [Math].
http://arxiv.org/abs/1510.07769
Serre, J.-P. (1980). Trees and Amalgams. In J.-P. Serre, Trees (pp. 1–68). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-61856-7_1
Hill, T. P. (2021). An Evolutionary Theory for the Variability Hypothesis.
ArXiv:1703.04184 [q-Bio].
http://arxiv.org/abs/1703.04184
Albuquerque, P. (1999). Patterson-Sullivan Theory in Higher Rank Symmetric Spaces.
Geometric & Functional Analysis GAFA,
9(1), 1–28.
https://doi.org/10.1007/s000390050079
Kadison, R. V., & Ringrose, J. R. (1972). Cohomology of operator algebras. III : reduction to normal cohomology.
Bulletin de la Société Mathématique de France,
100, 73–96.
https://doi.org/10.24033/bsmf.1731
Kadison, R. V., & Ringrose, J. R. (1971). Cohomology of operator algebras II. Extended cobounding and the hyperfinite case.
Arkiv För Matematik,
9(1–2), 55–63.
https://doi.org/10.1007/BF02383637
Kadison, R. V., & Ringrose, J. R. (1971). Cohomology of operator algebras: I. Type I von Neumann algebras.
Acta Mathematica,
126(none), 227–243.
https://doi.org/10.1007/BF02392032
Pop, F., & Smith, R. R. (2010). Vanishing of second cohomology for tensor products of type II1 von Neumann algebras.
Journal of Functional Analysis,
258(8), 2695–2707.
https://doi.org/10.1016/j.jfa.2010.01.013
Christensen, E., Pop, F., Sinclair, A., & Smith, R. (2003). Hochschild Cohomology Of Factors With Property Gamma. Annals of Mathematics, 158, 635–659.
Hochschild cohomology of factors with property $\Gamma$ | Annals of Mathematics. (n.d.). Retrieved September 4, 2021, from
https://annals.math.princeton.edu/2003/158-2/p07
Cameron, J. (2009). Hochschild cohomology of II1 factors with Cartan maximal abelian subalgebras.
Proceedings of the Edinburgh Mathematical Society,
52, 287–295.
https://doi.org/10.1017/S0013091507000053
Cameron, J. (2009). Hochschild cohomology of II1 factors with Cartan maximal abelian subalgebras.
Proceedings of the Edinburgh Mathematical Society.
https://doi.org/10.1017/S0013091507000053
Johnson, B. E., Kadison, R. V., & Ringrose, J. R. (1972). Cohomology of operator algebras. III : reduction to normal cohomology.
Bulletin de La SociéTé MathéMatique de France,
79, 73–96.
https://doi.org/10.24033/bsmf.1731
Sinclair, A. M., & Smith, R. R. (1998). Hochschild Cohomology for Von Neumann Algebras with Cartan Subalgebras.
American Journal of Mathematics,
120(5), 1043–1057.
https://www.jstor.org/stable/25098635
Sinclair, A. M., & Smith, R. R. (1998). Hochschild Cohomology for Von Neumann Algebras with Cartan Subalgebras.
American Journal of Mathematics,
120(5), 1043–1057.
https://www.jstor.org/stable/25098635
Qian, W., & Shen, J. (2014). Hochschild cohomology of type II$_1$ von Neumann algebras with Property $\Gamma$.
ArXiv:1407.0664 [Math].
http://arxiv.org/abs/1407.0664
Sinclair, A. M., & Smith, R. R. (1995). Hochschild Cohomology of Von Neumann Algebras. Cambridge University Press.
Eynard, B. (2014). A short overview of the “Topological recursion.”
ArXiv:1412.3286 [Hep-Th, Physics:Math-Ph].
http://arxiv.org/abs/1412.3286
Pimsner, M. V. (1986). KK-groups of crossed products by groups acting on trees.
Inventiones Mathematicae,
86(3), 603–634.
https://doi.org/10.1007/BF01389271
Pimsner, M. (1986).
KK-groups of crossed products by groups acting on trees.
https://doi.org/10.1007/BF01389271
Rieffel, M. (1982).
Applications of strong Morita equivalence for transofrmation C*-algebras.
38(1).
https://math.berkeley.edu/~rieffel/papers/applications.pdf
Kloeckner, B. (2010). Symmetric spaces of higher rank do not admit differentiable compactifications.
Mathematische Annalen,
347(4), 951–961.
https://doi.org/10.1007/s00208-009-0464-z
Paradan, P.-E. (2009). Symmetric spaces of the non-compact type: Lie groups.
Séminaires et Congrès,
Géométries à courbure négative ou nulle, groupes discrets et rigidités(18), 39–76.
https://hal.archives-ouvertes.fr/hal-00773255
Connes, A., & Skandalis, G. (1984). The Longitudinal Index Theorem for Foliations.
Publications of the Research Institute for Mathematical Sciences,
20(6), 1139–1183.
https://doi.org/10.2977/prims/1195180375
Schroeder, M. (2010). Patterson-Sullivan distributions for symmetric spaces of the noncompact type.
ArXiv:1012.1113 [Math].
http://arxiv.org/abs/1012.1113
Helgason, S. (1979). Differential Geometry, Lie Groups, and Symmetric Spaces. Academic Press.
Emerson, H., & Meyer, R. (2006). Euler characteristics and Gysin sequences for group actions on boundaries.
Mathematische Annalen,
334(4), 853–904.
https://doi.org/10.1007/s00208-005-0747-y
Blackadar, B. (1986). K-Theory for Operator Algebras. Springer-Verlag. https://doi.org/10.1007/978-1-4613-9572-0
Ji, L., & Macpherson, R. (2002). Geometry of compactifications of locally symmetric spaces.
Annales de l’institut Fourier,
52(2), 457–559.
https://doi.org/10.5802/aif.1893
Ulsnaes, T. (n.d.). Note series.
Ulsnaes, T. (2021). The Karpelevic compactification.
Jin, X. (2021). Homological Mirror Symmetry for the universal centralizers I: The adjoint group case.
ArXiv:2107.13395 [Math-Ph].
http://arxiv.org/abs/2107.13395
Soule, C. (2004).
An introduction to arithmetic groups.
https://hal.archives-ouvertes.fr/hal-00001348
Rosenberg, J. M., & Schochet, C. (1986). The Künneth theorem and the universal coefficient theorem for equivariant K-theory and KK-theory. American Mathematical Society.
Rieffel, M. A. (2002). Group C∗-Algebras as Compact Quantum Metric Spaces. Documenta Mathematica, 48.
Ulsnaes, T. (n.d.). Compactifications of symmetric spaces and their applications. X ., 52.
Ulsnaes, T. (n.d.). An example of the index of a Rockland operator on a contact manifold. 68.
Ulsnaes, T. (n.d.). A simple proof of the Hard Lefschetz theorem. 37.
Ulsnaes, T. (n.d.). Pensum MATH4450 Videreg˚aende Funksjonal analyse V˚ar 2017. 22.
Videregående Funksjonalanalyse. (n.d.). Retrieved June 22, 2021, from
https://www.overleaf.com/project/59920ace6080cd3eb133870e
![]() towards irregular points on the geodesic boundary
towards irregular points on the geodesic boundary ![]() of a non-compact symmetric space
of a non-compact symmetric space![]() , and a point
, and a point ![]() . If
. If ![]() is a geodesic in
is a geodesic in ![]() with
with ![]() , let
, let ![]() be a normal neighborhood of
be a normal neighborhood of ![]() constructed as the parallel translates along
constructed as the parallel translates along ![]() of a fixed ball
of a fixed ball ![]() . We can easily construct a bump function
. We can easily construct a bump function ![]() with the following properties
with the following properties only depends on the distance from
only depends on the distance from  ,
,  is zero on
is zero on  and
and  on a neighborhood of
on a neighborhood of  .
.![]() is the real hyperbolic plane, with the Poincare disc model and
is the real hyperbolic plane, with the Poincare disc model and ![]() , then the geodesic ray from
, then the geodesic ray from ![]() is just a straight line through the origin. The neighborhood
is just a straight line through the origin. The neighborhood ![]() is a tube around the geodesic line which shrinks in diameter as it gets closer to the boundary, where it collapses to a single point. If we assume the function
is a tube around the geodesic line which shrinks in diameter as it gets closer to the boundary, where it collapses to a single point. If we assume the function ![]() could be extended to the closure of the disc (which is the geodesic compactification of
could be extended to the closure of the disc (which is the geodesic compactification of ![]() ), then we are faced with the following difficult question: What are the limit points of the set
), then we are faced with the following difficult question: What are the limit points of the set ![]() ?
?![]() and since
and since ![]() collapses to a single point on the boundary, we conclude that
collapses to a single point on the boundary, we conclude that ![]() intersects the boundary at precisely two points, namely the limit points of
intersects the boundary at precisely two points, namely the limit points of ![]() . Thus we find that by choosing what sequence in
. Thus we find that by choosing what sequence in ![]() converges to the boundary point of
converges to the boundary point of ![]() , the “extension” of
, the “extension” of ![]() can attain any value between
can attain any value between ![]() and
and ![]() on these boundary points. Thus the extension cannot be continuous.
on these boundary points. Thus the extension cannot be continuous.![]() on the geodesic boundary is called irregular if the corresponding geodesic
on the geodesic boundary is called irregular if the corresponding geodesic ![]() is contain in at least two maximal totally geodesic submanifolds of
is contain in at least two maximal totally geodesic submanifolds of ![]() .
.![]() be a non-compact symmetric space, let
be a non-compact symmetric space, let ![]() be any point. Let
be any point. Let ![]() be the union of all geodesic rays from
be the union of all geodesic rays from ![]() to
to ![]() (the irregular points on the geodesic boundary). Let
(the irregular points on the geodesic boundary). Let ![]() denote a normal neighborhood of
denote a normal neighborhood of ![]() of radius
of radius ![]() in the metric of
in the metric of ![]() . This is just the union of all parallel translates of a fixed ball
. This is just the union of all parallel translates of a fixed ball ![]() along the irregular geodesic rays from
along the irregular geodesic rays from ![]() . Let
. Let ![]() be a continuous bump function which is
be a continuous bump function which is ![]() on
on ![]() and zero outside of
and zero outside of ![]() and assume
and assume ![]() only depends on the distance from
only depends on the distance from ![]() . The function
. The function ![]() is then a bump function for the set
is then a bump function for the set ![]() of geodesic rays from
of geodesic rays from ![]() going towards irregular boundary points.
going towards irregular boundary points.![]() be given by
be given by![]()
![]() is clearly continuous and bounded on
is clearly continuous and bounded on ![]() . Since it is a very natural construction, it may be interesting to look at what function we get on the boundary when we extend
. Since it is a very natural construction, it may be interesting to look at what function we get on the boundary when we extend ![]() to certain compactifications of
to certain compactifications of ![]() .
.![]() converges radially to a well defined function on
converges radially to a well defined function on ![]() which is
which is ![]() on the regular boundary points and
on the regular boundary points and ![]() on the irregular boundary points. Though we should emphasize that the extension is radial, and not continuous. Continuous extensions cannot exist, as the next lemma shows
on the irregular boundary points. Though we should emphasize that the extension is radial, and not continuous. Continuous extensions cannot exist, as the next lemma shows![]() . Then it is easy to check that
. Then it is easy to check that ![]() converges to
converges to ![]() . Since
. Since ![]() is an extension of
is an extension of ![]() , we have
, we have ![]() . Since
. Since ![]() is assumed to be independent of choice of convergent sequence to
is assumed to be independent of choice of convergent sequence to ![]() , it follows that
, it follows that ![]() exists and is independent of choice of sequence
exists and is independent of choice of sequence ![]() .
. ![]() is real valued and extends to a function on
is real valued and extends to a function on ![]() which has a jump discontinuity at
which has a jump discontinuity at ![]() (from
(from ![]() to
to ![]() in
in ![]() ), then some sequence in
), then some sequence in ![]() converges to
converges to ![]() . Hence the extension is not well defined at
. Hence the extension is not well defined at ![]() .
.![]() converges to a well defined function on
converges to a well defined function on ![]() but not to the whole geodesic compactification
but not to the whole geodesic compactification ![]() . To this end let
. To this end let![]()
![]() in
in ![]() . We have –
. We have –![]()
![]()
![]() to the unique geodesic ray from
to the unique geodesic ray from ![]() to
to ![]() . The set
. The set ![]() is thus open in
is thus open in ![]() .
.![]() of radius
of radius ![]() along a geodesic ray, the “size of ”
along a geodesic ray, the “size of ” ![]() as seen from a fixed observer goes to zero. Put differently, the maximal angle between geodesic rays from the observer to two points in the ball goes to zero as
as seen from a fixed observer goes to zero. Put differently, the maximal angle between geodesic rays from the observer to two points in the ball goes to zero as ![]() is translated away from the observer.
is translated away from the observer.![]() as seen from
as seen from ![]() will get closer and closer to the set
will get closer and closer to the set ![]() . Put differently, the maximal angle between geodesic rays from
. Put differently, the maximal angle between geodesic rays from ![]() and
and ![]() will tend to zero.
will tend to zero. ![]() is a sequence converging to
is a sequence converging to ![]() , then, using the definition of the topology on
, then, using the definition of the topology on ![]() , if
, if ![]() denotes the unit vector corresponding to the geodesic ray from
denotes the unit vector corresponding to the geodesic ray from ![]() to
to ![]() and
and ![]() the geodesic ray going to
the geodesic ray going to ![]() , then the
, then the ![]() in
in ![]() . Picking any open neighborhood
. Picking any open neighborhood ![]() of
of ![]() such that
such that ![]() . Then for
. Then for ![]() large enough we have
large enough we have ![]() and
and ![]() for all
for all ![]() , where the last part follow from the above lemma. It follows that the geodesic ray converging to
, where the last part follow from the above lemma. It follows that the geodesic ray converging to ![]() is eventually outside of
is eventually outside of ![]() and
and ![]() . So
. So ![]() extends to
extends to ![]() . Note that the sequence
. Note that the sequence ![]() was arbitrary in the above example, so
was arbitrary in the above example, so ![]() extends continuously to
extends continuously to ![]() .
.![]() . If
. If ![]() , then
, then ![]() for some
for some ![]() . But if
. But if ![]() this does not imply
this does not imply ![]() . It is actually possible to check that
. It is actually possible to check that ![]() can converge to any value in
can converge to any value in ![]() by converging along different sequences
by converging along different sequences ![]() to the same irregular point. What we mean by extending
to the same irregular point. What we mean by extending ![]() to
to ![]() is that we extend it along geodesic rays from
is that we extend it along geodesic rays from ![]() . In this case, there is only one value
. In this case, there is only one value ![]() can attain at any point in
can attain at any point in ![]() and we are done.
and we are done.![]() does however extend to a continuous function on the Karpelevich compactification
does however extend to a continuous function on the Karpelevich compactification ![]() . Let’s see why. The book of Borel and Ji is our reference for the definitions of the Karpelevich compactification.
. Let’s see why. The book of Borel and Ji is our reference for the definitions of the Karpelevich compactification. ![]() can be written as tuples
can be written as tuples ![]() , where
, where ![]() and
and ![]() and
and ![]() is the Karpelevich compactification of the boundary symmetric space at
is the Karpelevich compactification of the boundary symmetric space at ![]() , meaning if
, meaning if ![]() is the parabolic subgroup stabilizing
is the parabolic subgroup stabilizing ![]() , then
, then ![]()
![]() converge to a boundary point
converge to a boundary point ![]() . Then, one can always express
. Then, one can always express ![]() as
as![]()
![]() ,
, ![]() is a representative in
is a representative in ![]() and
and ![]() are such that
are such that ![]() (mentioned in the proof of Proposition I.15.6 of but also implicit in the definition of the Karpelevich compactification on p. 53).
(mentioned in the proof of Proposition I.15.6 of but also implicit in the definition of the Karpelevich compactification on p. 53).![]() converges to
converges to ![]() if and only if
if and only if in
in  or equivalently
or equivalently  in
in  .
. in
in  .
.![]() be a sequence converging to
be a sequence converging to ![]() where
where ![]() and
and ![]() (recall that we assume
(recall that we assume ![]() has rank 2!). Let
has rank 2!). Let ![]() be the geodesic centered at
be the geodesic centered at ![]() in the direction of
in the direction of ![]() , i.e.
, i.e. ![]() and
and ![]() . Recall that
. Recall that ![]() is the Cartan subgroup of
is the Cartan subgroup of ![]() , hence
, hence ![]() is a limit point of
is a limit point of ![]() in
in ![]() , and we can write
, and we can write ![]() for some
for some ![]() (if not we would have to write
(if not we would have to write ![]() for some
for some ![]() using the polar decomposition of
using the polar decomposition of ![]() described in a previous blog post).
described in a previous blog post).
![]() (so
(so ![]() uniformly in
uniformly in ![]() ) and
) and ![]() is a totally geodesic submanifold of
is a totally geodesic submanifold of ![]() orthogonal to
orthogonal to ![]() at
at ![]() . Since
. Since ![]() converges in the geodesic compactification of
converges in the geodesic compactification of ![]() it follows that
it follows that ![]() converges or diverges to
converges or diverges to ![]() . Either way the the distance
. Either way the the distance ![]() converges in
converges in ![]() and if
and if ![]() is another sequence converging to
is another sequence converging to ![]() with
with![]()
![]() in
in ![]() as the limit keeps track of the distance from
as the limit keeps track of the distance from ![]() . This is all we need to ensure that
. This is all we need to ensure that ![]() is well defined and does not depend on the choice of convergent sequence in
is well defined and does not depend on the choice of convergent sequence in ![]() . We have thus proved
. We have thus proved![]() where the function
where the function ![]() (or
(or ![]() ) could not be extended and “blown” them up by gluing in the boundary symmetric spaces
) could not be extended and “blown” them up by gluing in the boundary symmetric spaces ![]() at these points. The extension of the function
at these points. The extension of the function ![]() is then a bump function of some open set in
is then a bump function of some open set in ![]() where
where ![]() runs over all limit points of irregular boundary points.
runs over all limit points of irregular boundary points.